Abstract
Amino acids (AAs) are the basic building blocks of proteins and regulate the body's metabolism. The mechanical properties of proteins play an essential role in their functionalities in addition to their structure and dynamic properties. They are paramount in understanding the flexibility, rigidity, and ability to resist deformation. It is critical to investigate the mechanical properties of the twenty standard AAs that comprise the protein. Herein, we have developed a computational approach based on a detailed ab initio quantum mechanical method based on density functional theory that can calculate the mechanical properties of strategically designed models of solvated AAs. This de novo approach has been applied to twenty standard amino acids as the first step towards exploring the mechanical properties of super-soft biomolecular systems. The calculated properties include the Young's modulus, shear modulus, bulk modulus, and Poisson's ratio under different strains. We have identified AAs with relatively higher/lower compressibility, rigidity, flexibility, stretchability, and hardness based on their mechanical properties. Our findings are valuable as the starting point for future studies on large peptides or small proteins.
Keywords
1. Introduction
Amino acids (AAs) are the basic units of proteins. In fact, proteins are long chains of amino acids. Both AAs and proteins are building blocks of life. AAs are used extensively in a variety of industrial and medical applications[1]. Structurally, each AA is an organic compound that has a central α-carbon atom linked together with a basic amino group, a carboxylic acid group, a hydrogen atom and an R-group, or the side-chain group. The R-group characterizes the chemical nature of each AA. There are 20 canonical AAs as listed in Table 1. They are classified in different groups depending in their side chains such as aliphatic hydrophobic (Ala, Gly, Ile, Leu, Met, Pro, and Val), aromatic hydrophobic (Phe and Trp), polar with neutral side chain (Asn, Cys, Gln, Ser, Thr, and Tyr), acidic with negatively charged side chain (Asp and Glu), basic with positively charged side chain (Arg, Lys, and His). Some AAs have special or unique properties such as Cys, Gly, Met, Pro, and Ser. Cys has a very reactive sulfhydryl group (thiol group) on its sidechain. This free thiol group can react with another thiol from another Cys residue to form a disulfide bond. This renders Cys a permanent component of protein primary structure and plays a crucial role in protein-folding pathways[2]. In addition, the thiol sidechain in Cys also participates in enzymatic reactions[3]. Gly is another unique AA and is classified as hydrophobic because it contains only one hydrogen atom in the sidechain making Gly the most flexible AA. Met is also classified as a hydrophobic AA and contains sulfur (S) on its sidechain. This S in Met can interact with other molecule to form S-containing molecules. S-containing molecules have a variety of functions including tissue protection, modifying our DNA and maintaining proper functioning of cells[2]. In addition, Met plays a critical role in initiating the synthetic process of new proteins[2]. Pro is unique since its sidechain is connected to the protein backbone twice, forming a five-membered nitrogen-containing ring. This distinctive cyclic structure of Pro gives an exceptional conformational rigidity compared to other AAs[4]. Ser is important in metabolism by participating in the biosynthesis of purines and pyrimidines of nucleic acids. This is unique among the 20 AAs in that it is encoded by two disjoint sets of codons[5].
| AAs | No. of H2O | No. of atoms |
| Ala | 26 | 91 |
| Arg | 41 | 149 |
| Asn | 31 | 110 |
| Asp | 31 | 109 |
| Cys | 25 | 89 |
| Gln | 36 | 128 |
| Glu | 34 | 121 |
| Gly | 19 | 67 |
| His | 38 | 134 |
| Ile | 30 | 112 |
| Leu | 31 | 115 |
| Lys | 38 | 138 |
| Met | 35 | 125 |
| Phe | 35 | 128 |
| Pro | 30 | 107 |
| Ser | 25 | 89 |
| Thr | 30 | 107 |
| Trp | 48 | 171 |
| Tyr | 36 | 132 |
| Val | 30 | 109 |
AAs: amino acids.
AAs are environmentally friendly, inexpensive, and easily achievable in high purity. They are used as inhibitors or inhibitor-modifying reagents for calcite scales[6]. There are density functional theory (DFT)-based calculations of AAs to evaluate their chemical reactivity[7] and its uses as green corrosion inhibitors[8-11]. Currently, there are special interests in the area of molecular solids used in biocompatible nanodevices[12,13]. DFT-based studies have calculated chemical hardness of AAs, using the energy of highest occupied molecular orbital and lowest unoccupied molecular orbital, which helps to identify their reactivity[6]. There exists a study calculating Vickers microhardness on crystals with doped AAs[14]. AAs crystals have been explored as supramolecular materials for their potential applications in photonic device, stretchable electronics, and power generation[15]. Ji et al.[15] have measured Young's modulus of three AAs crystals. Azuri et al. calculated Young's modulus of crystalline structure of AAs such as α-glycine, γ-glycine, L-alanine, DL-serine, and glycylglycine[16]. Matveychuk et al. calculated Young's modulus, linear compressibility, shear modulus and Poisson's ratio on crystalline AA hydrogen maleates with prospect of designing new crystals[17]. To our knowledge, there are lack of studies regarding the mechanical properties of the canonical 20 AAs. This study tries to fill that gap. Understanding mechanical properties of soft tissues enable us to develop realistic simulations for surgical planning and training[18]. There is research going on in calculating mechanical properties of soft tissues. For example, Miller et al. studied the extension of soft brain tissue[19,20]. Chui et al.[21,22], Roan et al.[23], and Gao et al.[18] investigated liver tissues. In addition, Lee et al.[24] have studied micromechanical properties of complex collagenous tissue, Serwane et al.[25] have studied mechanical properties of developing 3D tissue.
Proteins are vital for all biological processes. Understanding protein function requires a complete knowledge of its structural, dynamical, and mechanical behaviors[26]. Certain proteins change their biological functions when subjected to mechanical deformations[27]. These deformations are necessary to explain the molecular basis for many of the cellular processes involving mechano-sensing and mechano-transduction[27]. Hence, there is an urgent need to investigate the protein behavior under mechanical deformation. Changes in amino acid sequence may alter the mechanical properties of proteins in many aspects[28]. For example, altering the hydrophobic sidechains could influence the amount of energy required to deform the protein due to change in the attractive energy between side chains via their hydrophobicity[29-31]. Additionally, changing the charge in the sidechains could interrupt their ionic interactions via losing the salt bridges between them, resulting in destabilizing the protein stiffness[32,33].
These AAs drive the folding and forming intramolecular bonding in three-dimension (3D)[34]. There are different factors in AAs affecting protein folding such as their intrinsic nature upon which they are classified, hydrogen bonding, and van der Waals interactions[35]. Hence, the composition and the sequence of AAs are all essential for protein functions.
Mechanical properties are influenced by structural property of any materials including crystal, glass, water, etc. Protein or peptides differ from other materials as some of their regions could be more flexible than other regions. This could be due to the permutation and the combination of chain of different amino acids. Identifying the regions of flexibility and rigidity in peptides and proteins enable us to understand the mechanism of protein folding[36,37]. Using accurate method such as DFT to calculate mechanical properties of a protein or peptides is expensive[38]. Before we investigate more complex proteins, we start with simpler systems such as AAs. AAs are small biological molecules and applying strains are difficult to conduct experimentally. Among computational approaches, ab initio DFT calculation is known for its reliability and accuracy. In this work, we have calculated mechanical properties of 20 canonical AAs immersed in water using the ab initio method. The mechanical properties such as bulk modulus, shear modulus, Young's modulus, and Poisson's ratio have been calculated using 17 different strain percentages.
2. Models and Methods
The structures of the 20 AAs are derived from PubChem[39]. PubChem compound identification 5950 (Ala), 6322 (Arg), 6267 (Asn), 5960 (Asp), 5862 (Cys), 5961 (Gln), 33032 (Glu), 750 (Gly), 6274 (His), 6306 (Ile), 6106 (Leu), 5962 (Lys), 6137 (Met), 6140 (Phe), 145742 (Pro), 5951 (Ser), 6288 (Thr), 6305 (Trp), 6057 (Tyr), and 6287 (Val) were used. All AAs were solvated using Packmol[40] with solvation shell size of 3 Å for consistency. As the size of all AAs differ from each other so does the number of water molecules added in each AAs (Table 1). Gly is the smallest AA with only 19 water molecules added. Whereas Trp is the largest AA having 48 water molecules added. As an example, we show the ball and stick figure of solvated Ala in Figure 1. Water molecules were added for two reasons: 1) to mimic periodic boundary conditions in Vienna ab initio Simulation Package (VASP) calculation and 2) the presence of water is real in all biomolecular systems.
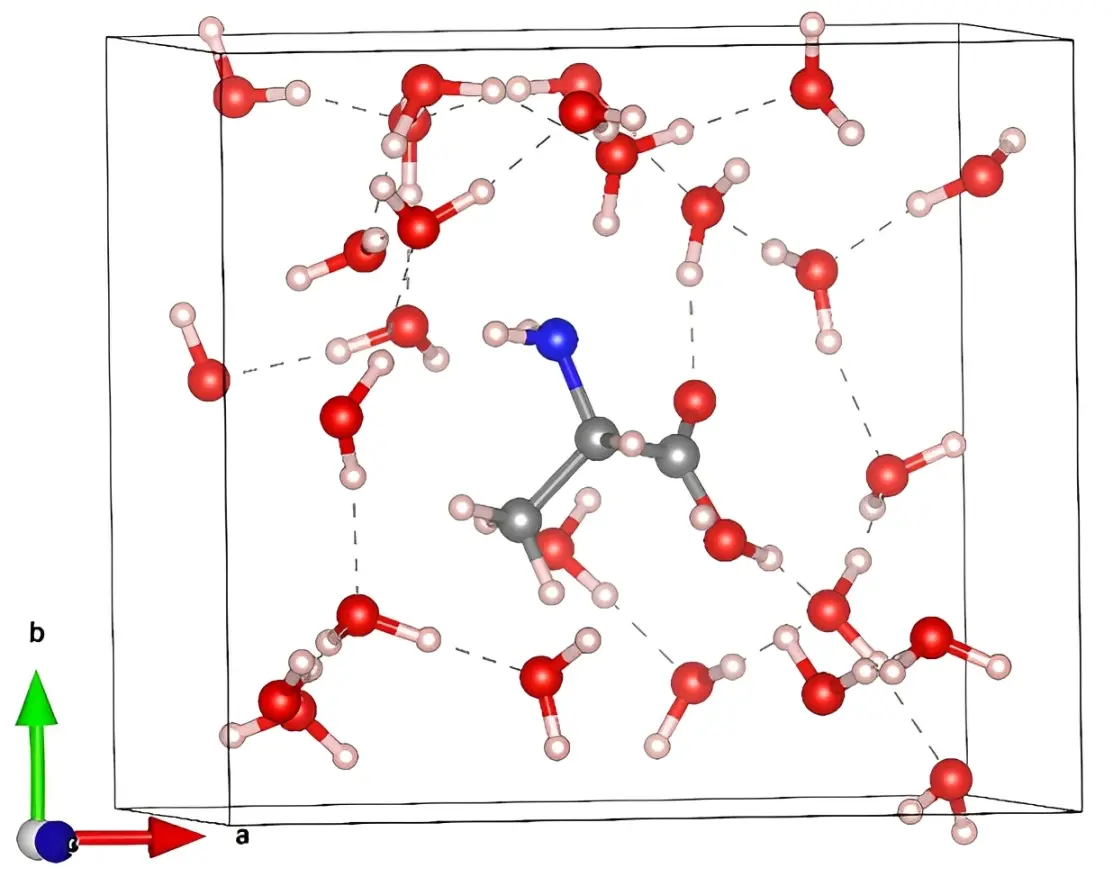
Figure 1. Ball and stick sketch of Ala in water box. Grey: C; red: O; blue: N; light pink: H.
We used the DFT-based package VASP[41] for optimization of solvated AAs. In VASP, we used projector augmented wave[42,43] method with Perdew-Burke-Ernzerhof (PBE)[42] exchange correlation functional within the generalized gradient approximation (GGA). PBE is one of the best GGA available in VASP. We are aware of vdW/dispersive corrections and will include them in our future research. We will then be able to identify if it makes any significant changes in mechanical properties.
We have experience in calculating mechanical properties for different materials ranging such as suolunite crystal and silica binding peptide[44], metal organic framework[45], crystals[46], glasses[47], and some complex system[48]. Based on our experience, we used energy cut off 600 eV with electronic convergence of 10-5 eV, ionic convergence of -10-3 eV, and a single k-point sampling. The fully optimized structure is then used to calculate the elastic coefficients Cij using VASP. Cij are calculated using the stress versus strain approach of Nielsen and Martin scheme[49]. A strain (ε) is applied to the optimized structure according to Hooks law:
where stress component σi (i = 1 to 6) is linearly dependent to the applied strain εj (j = 1 to 6) under small deformation. The stress tensors xx, yy, zz, yz, zx, and xy are used in corresponding strain. equation (1) gives six sets of linear equations with six components of stress and 21 elastic constants. In the current study, a wide range of strain (ε) is applied to each solvated AAs, they are ± 0.01%, ± 0.015%, ± 0.02%, ± 0.025%, ± 0.03%, ± 0.035%, ± 0.1%, ± 0.25%, ± 0.4%, ± 0.5%, ± 0.7%, ± 1%, ± 1.5%, ± 1.75%, ± 2%, ± 2.25%, and ± 2.5%. A general practice is to use the higher strain percentage for soft materials[50]. We used up to 2.5% strain. The calculated elastic constants Cij and compliance tensor Sij are used to calculate mechanical properties using Voigt's approach, Reuss approach, and Voigt-Reuss-Hill approximation.
The Voigt's approach[51] gives the upper limit of bulk modulus KVoifht and shear modulus GVoight.
The Reuss's approach[52] gives the lower limit of bulk modulus KReuss and shear modulus GReuss.
The Hill's approach average Voigt and Reuss approaches known as Voight-Reuss-Hill approximation[53].
where, E is Young's modulus and η is Poisson's ratio.
3. Results and Discussion
3.1 Mechanical properties of amino acids
We have calculated the mechanical properties of 20 solvated AAs models. These mechanical properties consist of bulk modulus (K), shear modulus (G), Young's modulus (E) and Poisson's ratio (η) as shown in Figure 2. Using trial-and-error technique each AA has mechanical property result for 17 strains: 0.01%, 0.015%, 0.02%, 0.025%, 0.03%, 0.035%, 0.1%, 0.25%, 0.4%, 0.5%, 0.7%, 1%, 1.5%, 1.75%, 2%, 2.25%, and 2.5%.
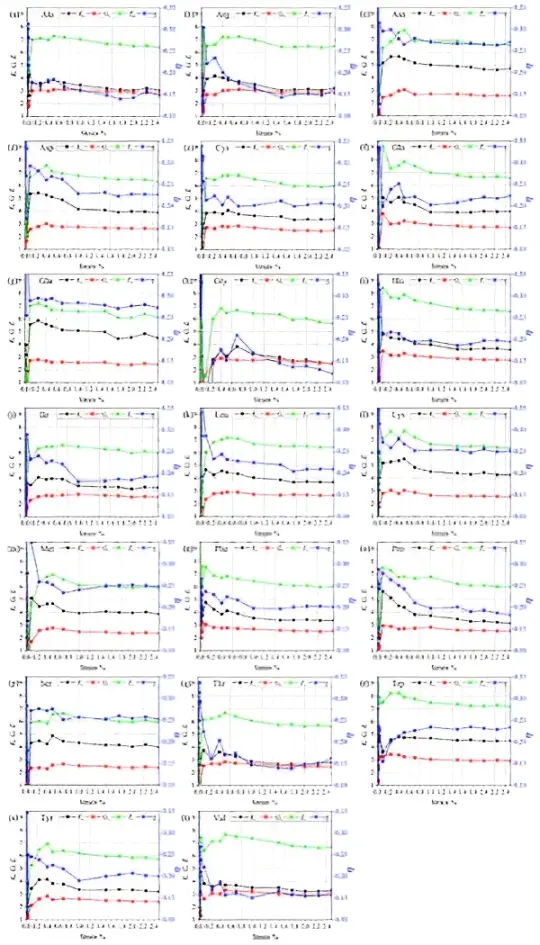
Figure 2. Bulk modulus, shear modulus, Young's modulus, and Poisson's ratio of 20 AAs in water box. AAs: amino acids.
Let us start with the first AA, Ala shown in Figure 2(a). The mechanical properties K, G, E and η have high fluctuations in strains from 0.01% to 0.1%. This is quite normal since the model structure is not a compact crystal but a solvated model. It contains voids that may lead to some uncertainty in the structure and properties. With the increase in the strain, the mechanical properties show much less fluctuations. A higher strain is known to be more suitable for soft materials with more reliable mechanical properties[50]. The mechanical properties from strain 0.1% to 2.5% show relatively closer and reasonable values, in contrast to the extreme fluctuations in the lower strains. We have chosen results from strain 0.1% to 2.5% for further analysis. K, G, E and η fluctuates in the range of 3.00-3.85 GPa, 2.78-3.08 GPa, 6.38-7.27 GPa, and 0.14-0.19 respectively. As the strain percentage increases, K, G and E show a decreasing trend with a notable peak at 0.5% strain. Poisson' s ratio (η) also shows a similar trend with slightly higher and lower peaks. We are unable to compare our values with any other studies, as there are no such experiments or theoretical calculations done.
Unlike other AAs, Gly (Figure 2h) and Met (Figure 2m) still have high fluctuations from 0.01% to 0.025% strain. Met has a slightly higher of 0.35 at 0.01% strain, which is reasonable. However, Gly has a negative η of -0.51 at 0.1% strain. Negative Poisson's ratio is plausible for auxetic materials. Instead of thinning, the material becomes thicker when stretched[54]. This value is not retained at higher strain. Besides, Gly does not show negative Poisson's ratio at strains lower than 0.1%. Hence, we consider this negative value an anomaly. Usually, materials have positive η since materials resist change in volume (measured by K) in comparison to resistance for change in the shape (measured by G). Another interesting fact about Gly and Met is they fall under special AAs having hydrophobic side chains.
Comparing all minimum and maximum values of mechanical properties for strains from 0.1% to 2.5% except for Gly, which was analyzed from 0.25% to 2.5%, we have following observations:
1) Poisson's ratio (η) for all solvated AAs falls under the range 0.12-0.35. Please note η for cork is 0[55], which means that if it is compressed or stretched the width or diameter remains the same. Whereas rubber with η of 0.5[56] implies that it requires smaller stress to deform. The lower the η, the more resistant is the material to deformation. Other examples that fall under closer η range as of AAs are polyacrylamide (0.24-0.33)[57] and cancerous skin tissue (0.43)[58]. However, these materials cannot be directly compared with the solvated AAs because η is just one property, and these materials may have different K, G and E. Gly has the lowest η of 0.12 at 2.5% strain whereas Met has the highest η of 0.35 at 0.1% strain.
2) Bulk modulus (K) for all solvated AAs models falls under the range of 2.47-5.85 GPa. Rubber has K of 1.5-2 GPa[59]. Some examples of K for liquids are water (2.15 GPa), Sulfuric acid (3.0 GPa), and Glycerine (4.35 GPa)[60]. The lower the bulk modulus K, the higher is the compression in the material. It is important to point out that the calculated bulk modulus range for solvated AAs can be closer or higher than water as this shows the behavior of AAs. Gly has lowest K of 2.47 GPa at 2.5% strain whereas Glu has highest K of 5.85 GPa at 2.5%.
3) Shear modulus (G) for all solvated AAs models falls in the range of 1.71-3.79 GPa. Some examples of G are: chalk (3.2 GPa)[61,62], wood (4 GPa)[63], and rubber (0.0006 GPa)[64]. G measures the rigidity of the material. Solvated AAs models have higher than that of rubber. AAs needs a little larger force to be deformed in comparison to rubber. Met has the lowest G of 1.71 GPa at 0.1% strain showing lower rigidity whereas Gln has highest G of 3.79 GPa at 0.1% strain showing higher rigidity.
4) Young's modulus (E) for all AAs falls under the range 4.62-9.08 GPa. Some examples of E are: medium-density fiberboard (4 GPa)[65], bone (14 GPa)[66], and rubber (0.01-0.1 GPa)[16]. E measures the tensile or compressive stiffness of material when the force is applied lengthwise. The higher the E the stiffer is the material. Rubber with lower E value shows its flexibility. Met has the lowest of 4.62 GPa at 0.1% strain showing relative flexibility whereas Gln has the highest E of 9.08 GPa at 0.1% strain showing less flexibility.
In the literature, Azuri et al.[16] reported Young's modulus of α-glycine, γ-glycine, L-alanine, DL-serine, and glycylglycine to be 26-94 GPa, 19-75 GPa, 15-68 GPa, 11-31 GPa, and 14-91 GPa respectively. Ji et al.[15] have calculated the Young's modulus of L-Phe and L-Tyr to be 13.6 ± 6.07 GPa and 177.03 ± 54.39 GPa. However, Azuri et al. and Ji et al. have studied mechanical properties of pure AAs crystals whereas we have studied AA solvated by water molecule hence the difference in results is obvious.
3.2 Strain percentage-based analysis
Analyzing 20 AAs mechanical properties in each strain percentage will show comparative nature of AA. Here in, we compare 20 AAs for each strain from 0.1% to 2.5% (11 data points) in Figure 3 which shows a clear picture of the highest and lowest mechanical properties, some of which were mentioned in section 3.1. There are few highs and lows in all mechanical properties in different strains, showing the peculiar nature of AAs. Let us start with strain 0.1% (Figure 3a). which has more fluctuations than other strains and falls under the boundary of lower deformation. At 0.1% strain Met has lowest G, lowest E, and highest η and Gln has highest G and E. Some AAs show a similar feature in most of the strain percentages. Following are our observations for the AAs with lower and higher mechanical properties.
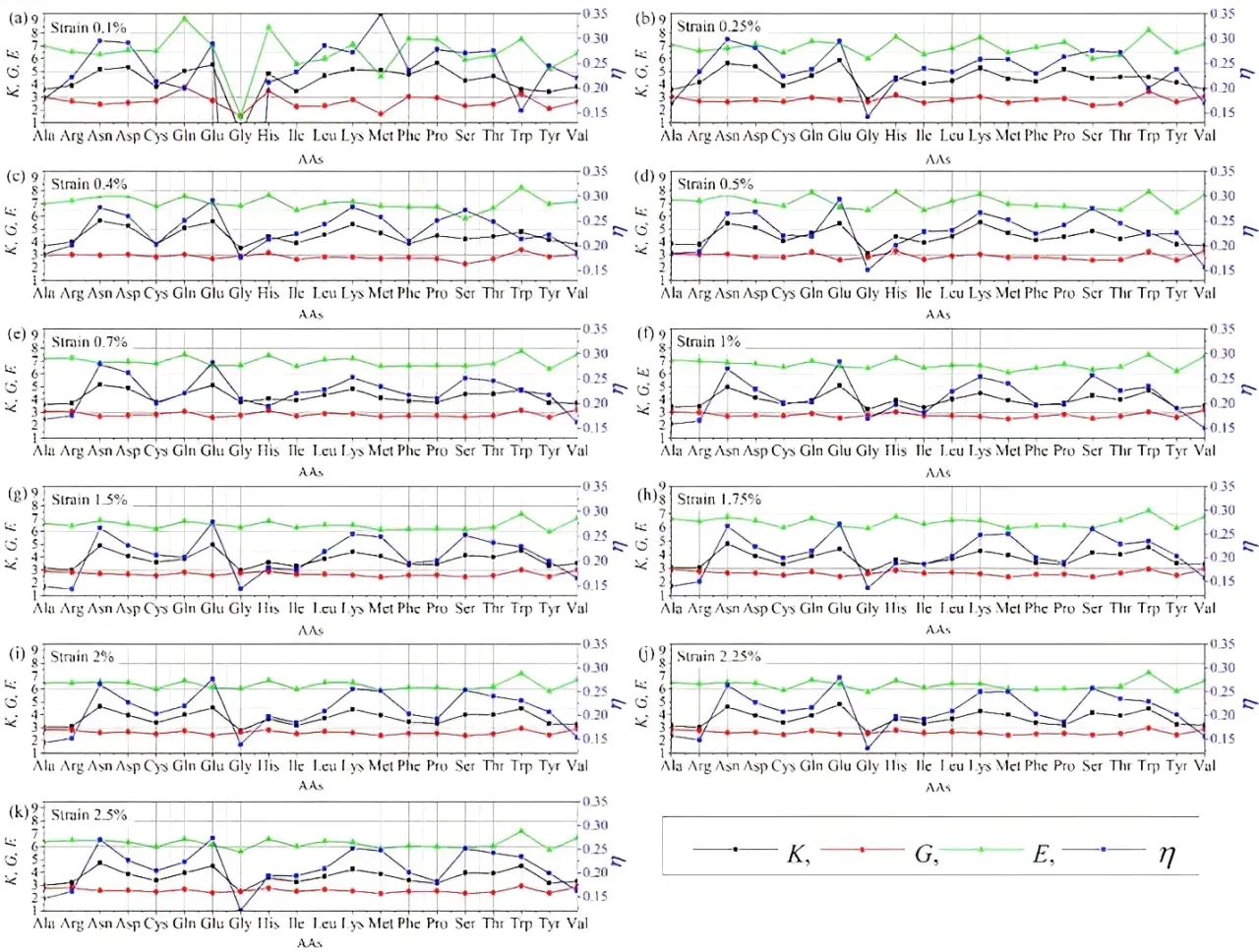
Figure 3. Bulk modulus, shear modulus, Young's modulus, and Poisson's ratio of solvated 20 AAs models for following strain percentages: (a) 0.1; (b) 0.25; (c) 0.4; (d)0.5; (e) 0.7; (f) 1; (g) 1.5; (h) 1.75; (i) 2; (j) 2.25; and (k) 2.5. AAs: amino acids.
1) Gly has the lowest K in most strains except at 0.7% indicating Gly is more compressible than other AAs. This could be because Gly is the simplest AA and has a hydrogen atom in its side chain[35]. Ala is the next simplest AA with side chain of a methyl group (-CH3)[35] and has lower K in 0.7%, 0.25%, 0.4%, 1.5%, 1.75%, 2%, 2.25%, and 2.5% strains. Glu and Asn show higher K at most strains. Glu is negatively charged and is known as one of the strongest helix formers[35]. Another negatively charged AA is Asp, which shows higher K at 0.1%, 0.25%, 0.4%, 0.5%, and 0.7% strains. It is interesting to notice both Asp and Asn, an uncharged derivative of Asp, have higher K. Asp contains carboxylic acid as a terminal whereas Asn contains carboxamide as a terminal. Trp with hydrophobic side chain shows higher K at 1%, 1.5%, 1.75%, 2%, 2.25%, and 2.5% strains. Pro shows highest K at 0.1%. However, Pro does not have higher K at other strains showing that some AAs may have different feature under different strains.
2) Ser and Met have lower G under most of the strains implying they are less rigid in nature. Ser has uncharged polar side chain and has hydroxyl group making it hydrophilic whereas Met has hydrophobic side chain. Another AA with hydrophobic side chain and lower under 0.1%, 0.5%, 0.7%, 1%, 1.5%, 1.75%, 2%, 2.25%, and 2.5% strain is Tyr. These hydrophobic AAs tend to form clusters to avoid contact with water and are known to stabilize soluble proteins. Glu, a negatively charged AA, also has lower G under strains 0.5%, 1%, 1.75%, 2%, and 2.5%. Val, Trp, and His have higher G at most strains. Both Val and Trp have hydrophobic side chains and His has positive side chains. Gln has higher G at 0.1%, 0.4%, and 0.7% strains, Ala has higher G at 1%, 1.5%, 1.75%, 2%, 2.25%, and 2.5% strains, and Arg has higher G at 2% and 2.5% strains. Gln has uncharged polar side chain, Ala has uncharged nonpolar side chain and Arg has positive side chains. These complex features imply that the basic classification of AAs is unable to explain their mechanical properties.
3) Met and Tyr have lower under most strains making them relatively flexible. In addition, Ser has lower E at 0.25%, 0.4%, 1%, 1.5%, 1.75%, 2%, and 2.5% strains. Some G and E follow similar trends i.e., Met, Tyr, and Ser also have lower G. Whereas Gly with lower E at 0.1%, 0.25%, 0.5%, 1%, 1.75%, 2.25%, and 2.5% strains has a lower K. Showing similar nature with higher G His, Trp, and Val also have higher E in most strains. Gln, with a higher G value, also has higher E at 0.1%, 0.5%, 0.7%, 2.25%, and 2.5% strains. His, Trp, Val, and Gln with relatively higher indicates their stiff nature.
Gly, Ala, and Val have lower η. Both Gly and Ala also have lower K and some K and η follow similar trends. Arg have lower η at 0.75, 1%, 1.5%, 1.75%, 2%, 2.25%, and 2.5%. With the higher K, Asn and Glu also have higher η under most strains. Met has a noticeably higher η at 0.1%. Met, Lys, and Ser also have higher η in most of the strain. However, Asn and Glu are relatively more stretchable.
Hardness HV has been used as the most important property of materials. We have calculated hardness HV using Tian et al.[67] formula HV = 0.92 k1.137 · G0.708, where k = G/K. Figure 4 shows hardness for all AAs. We can say that all 20 AAs fall under soft materials. For reference, diamond has a hardness of 95 GPa. The second hardest material is cubic boron nitride (66 GPa)[67]. Figure 4 shows that there is difference in hardness in different strain percentages like other mechanical properties. AAs with overall relatively higher hardness are Ala, Arg, Gly, and Val. Gln, Trp have relatively higher hardness at 0.1% strain. Asn, Glu, Ser, and Thr have lower hardness. Some AAs such as Leu, Met, and Tyr have lower hardness at 0.1% strain. This shows that some AAs can behave differently under different strains.
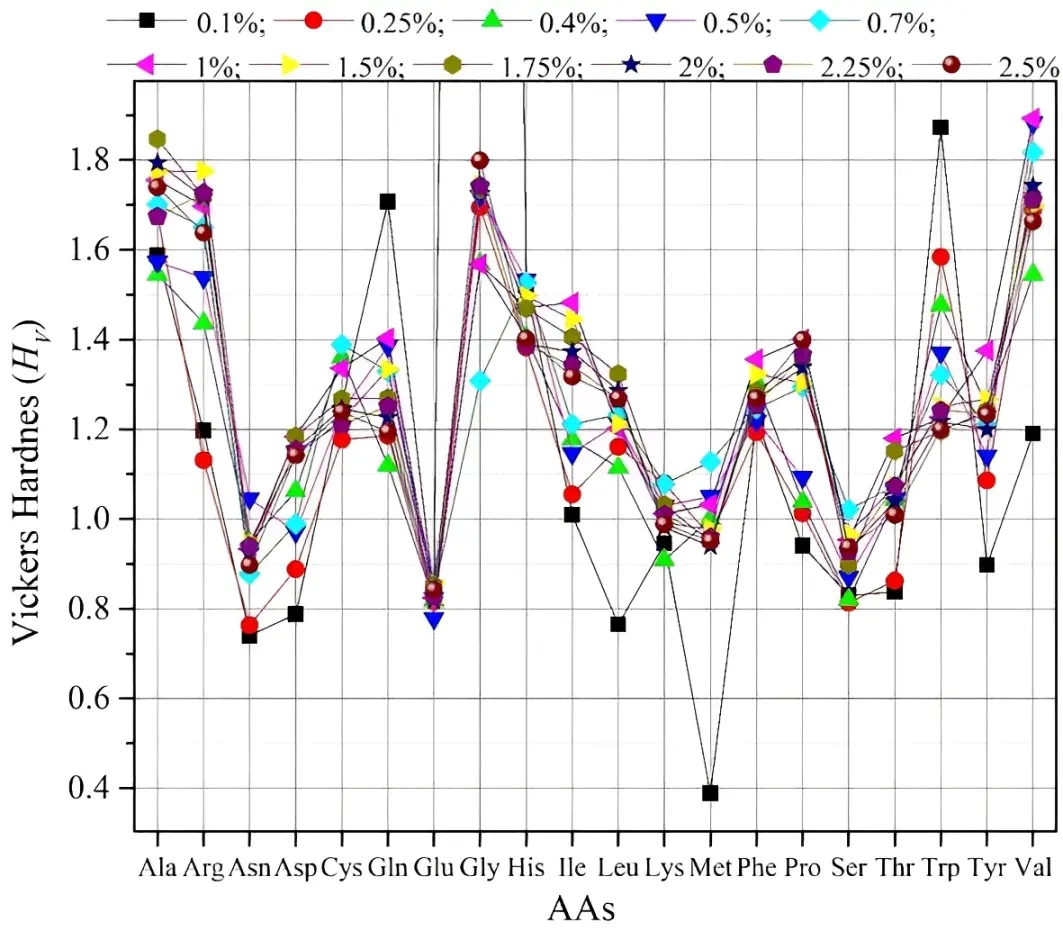
Figure 4. Vickers hardness HV for 20 solvated AAs models for 11 strain percentages. AAs: amino acids.
4. Conclusion
In this work, we have calculated mechanical properties of solvated AAs for the first time. Following are other observations:
1) Gly and Ala have relatively lower K whereas Glu, Asn, Asp, and Trp have higher K.
2) Ser, Met, Glu, and Tyr have relatively lower G whereas Val, Trp, His, and Ala have higher G.
3) Met, Tyr, and Gly have relatively lower E whereas His, Trp, Val have higher E.
4) Gly, Ala, Val, and Arg have low η whereas Asn and Glu have relatively high η.
5) All AAs are soft in nature based on lower HV. However, Ala, Arg, Gly, and Val have relatively high HV whereas Asn, Glu, Ser, and Thr have relatively low HV.
We conclude that some AAs retain their properties in most of the strains whereas some fluctuate. Even though the range of mechanical properties looks closely, they have slight differences. In addition, we observed no clear relationship between the classification of AAs and their mechanical properties. About 16 out of 20 AAs have some prominent feature either in K, G, E and η or in strain-based analysis. We would like to point out that, our work is just a starting point and we plan to calculate mechanical properties of a real biomolecules such as 1FUV[68,69]. 1FUV is a peptide sequence with the Arg-Gly-Asp (RGD). RGD has a higher affinity to a membrane protein called integrin hence RGD is used to target cancer cells. In addition, RGD has numerous applications in biomaterial design and biomedical devices. RGD is used as a candidate for wound healing, radiotracers in imaging, and implantable medical devices. The utilization of current result in analyzing the mechanical properties of 1FUV will be published in future. In addition, we will also focus on hydrogen bonding between AAs and water molecules as this also plays a discernable role in the mechanical properties using our experience of amino acids-amino acids bond pair[70] study in spike protein of SARS-CoV-2 via orthogonalized linear combination of atomic orbitals[71].
Acknowledgement
This research used the resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy by U.S. Department of Energy under Contract No. DE-AC03-76SF00098, DE-AC02-05CH11231 using NERSC award NERSC DDR-ERCAP0023727, and the Research Computing Support Services (RCSS) of the University of Missouri System.
Authors contribution
Adhikari P: Conducted the calculations, wrote the initial draft, editing and writing the manuscript.
Ching WY: Conceived the study, editing and writing the manuscript.
Jawad B: Editing and writing the manuscript.
Conflicts of interest
The authors declare there is no conficts of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Availability of data and materials
The data supporting the findings of this study are available within the article.
Funding
None.
Copyright
© The Author(s) 2023.
References
-
1. Xu Q, Deng H, Li X, Quan ZS. Application of amino acids in the structural modification of natural products: a review. Front Chem. 2021;9:650569.[DOI]
-
2. Brosnan JT, Brosnan ME. The sulfur-containing amino acids: an overview. J Nutr. 2006;136(6 Suppl):1636S-1640S.[DOI]
-
3. Song X, Dong B, Kong X, Wang C, Zhang N, Lin W. A sensitive and selective red fluorescent probe for imaging of cysteine in living cells and animals. Anal Methods. 2017;9(12):1891-1896.[DOI]
-
4. Huang F, Nau WM. A conformational flexibility scale for amino acids in peptides. Angew Chem Int Ed Engl. 2003;42(20):2269-2272.[DOI]
-
5. Schwartz GW, Shauli T, Linial M, Hershberg U. Serine substitutions are linked to codon usage and differ for variable and conserved protein regions. Sci Rep. 2019;9(1):17238.[DOI]
-
6. Jalab R, Saad MA, Hussein IA, Onawole AT. Calcite scale inhibition using environmental-friendly amino acid inhibitors: DFT investigation. ACS Omega. 2021;6(47):32120-32132.[DOI]
-
7. Brinzei M, Stefaniu A, Iulian O, Ciocirlan O. Density functional theory (DFT) and thermodynamics calculations of amino acids with polar uncharged side chains. Chem Proc. 2021;3(1):56.[DOI]
-
8. Dehdab M, Shahraki M, Habibi-Khorassani SM. Theoretical study of inhibition efficiencies of some amino acids on corrosion of carbon steel in acidic media: green corrosion inhibitors. Amino Acids. 2016;48(1):291-306.[DOI]
-
9. Frau J, Glossman-Mitnik D. Conceptual DFT. Conceptual DFT descriptors of amino acids with potential corrosion inhibition properties calculated with the latest minnesota density functionals. Front Chem. 2017;5:16.[DOI]
-
10. Fu J, Li S, Wang Y, Cao L, Lu L. Computational and electrochemical studies of some amino acid compounds as corrosion inhibitors for mild steel in hydrochloric acid solution. J Mater Sci. 2010;45:6255-6265.[DOI]
-
11. Kaya S, Tüzün B, Kaya C, Obot IB. Determination of corrosion inhibition effects of amino acids: quantum chemical and molecular dynamic simulation study. J Taiwan Inst Chem Eng. 2016;58:528-535.[DOI]
-
12. Kol N, Adler-Abramovich L, Barlam D, Shneck RZ, Gazit E, Rousso I. Self-assembled peptide nanotubes are uniquely rigid bioinspired supramolecular structures. Nano Lett. 2005;5(7):1343-1346.[DOI]
-
13. Niu L, Chen X, Allen S, Tendler SJB. Using the bending beam model to estimate the elasticity of diphenylalanine nanotubes. Langmuir. 2007;23(14):7443-7446.[DOI]
-
14. Dave DJ, Parikh KD, Joshi MJ. Vickers micro-hardness studies of amino acids (L-histidine, L-threonien and DL-methionine) doped KDP crystals. Adv Mater Res. 2013;665:172-178.[DOI]
-
15. Ji W, Xue B, Arnon ZA, Yuan H, Bera S, Li Q, et al. Rigid tightly packed amino acid crystals as functional supramolecular materials. ACS Nano. 2019;13(12):14477-14485.[DOI]
-
16. Azuri I, Meirzadeh E, Ehre D, Cohen SR, Rappe AM, Lahav M, et al. Unusually large young's moduli of amino acid molecular crystals. Angew Chem Int Ed Engl. 2015;54(46):13566-13570.[DOI]
-
17. Matveychuk YV, Bartashevich EV, Tsirelson VG. How the H-bond layout determines mechanical properties of crystalline amino acid hydrogen maleates. Cryst Growth Des. 2018;18(6):3366-3375.[DOI]
-
18. Gao Z, Desai JP. Estimating zero-strain states of very soft tissue under gravity loading using digital image correlation. Med Image Anal. 2010;14(2):126-137.[DOI]
-
19. Miller K. How to test very soft biological tissues in extension? J Biomech. 2001;34(5):651-657.[DOI]
-
20. Miller K, Chinzei K. Mechanical properties of brain tissue in tension. J Biomech. 2002;35(4):483-490.[DOI]
-
21. Chui C, Kobayashi E, Chen X, Hisada T, Sakuma I. Combined compression and elongation experiments and non-linear modelling of liver tissue for surgical simulation. Med Biol Eng Comput. 2004;42(6):787-798.[DOI]
-
22. Chui C, Kobayashi E, Chen X, Hisada T, Sakuma I. Transversely isotropic properties of porcine liver tissue: experiments and constitutive modelling. Med Biol Eng Comput. 2007;45:99-106.[DOI]
-
23. Roan E, Vemaganti K. The nonlinear material properties of liver tissue determined from no-slip uniaxial compression experiments. J Biomech Eng. 2007;129(3):450-456.[DOI]
-
24. Lee W, Moghaddam AO, Shen S, Phillips H, McFarlin BL, Johnson AJW, et al. An optomechanogram for assessment of the structural and mechanical properties of tissues. Sci Rep. 2021;11:324.[DOI]
-
25. Serwane F, Mongera A, Rowghanian P, Kealhofer DA, Lucio AA, Hockenbery ZM, et al. In vivo quantification of spatially varying mechanical properties in developing tissues. Nat Methods. 2017;14(2):181-186.[DOI]
-
26. Yang LQ, Sang P, Tao Y, Fu YX, Zhang KQ, Xie YH, et al. Protein dynamics and motions in relation to their functions: several case studies and the underlying mechanisms. J Biomol Struct Dyn. 2014;32(3):372-393.[DOI]
-
27. Bao G. Protein mechanics: a new frontier in biomechanics. Exp Mech. 2009;49:153-164.[DOI]
-
28. Caplan MR, Schwartzfarb EM, Zhang S, Kamm RD, Lauffenburger DA. Effects of systematic variation of amino acid sequence on the mechanical properties of a self-assembling, oligopeptide biomaterial. J Biomater Sci Polym Ed. 2002;13(3):225-236.[DOI]
-
29. Rose GD, Geselowitz AR, Lesser GJ, Lee RH, Zehfus MH. Hydrophobicity of amino acid residues in globular proteins. Science. 1985;229(4716):834-838.[DOI]
-
30. Roach P, Farrar D, Perry CC. Interpretation of protein adsorption: surface-induced conformational changes. J Am Chem Soc. 2005;127(22):8168-8173.[DOI]
-
31. de Jesus AJ, Allen TW. The role of tryptophan side chains in membrane protein anchoring and hydrophobic mismatch. Biochim Biophys Acta. 2013;1828(2):864-876.[DOI]
-
32. Hocky GM, Baker JL, Bradley MJ, Sinitskiy AV, De La Cruz EM, Voth GA. Cations stiffen actin filaments by adhering a key structural element to adjacent subunits. J Phys Chem B. 2016;120(20):4558-4567.[DOI]
-
33. Schepers AV, Lorenz C, Köster S. Tuning intermediate filament mechanics by variation of pH and ion charges. Nanoscale. 2020;12(28):15236-15245.[DOI]
-
34. Nature Education. Protein structure [Internet]. Available from: https://www.nature.com/protein-structure-14122136/
-
35. Berg JM, Tymoczko JL, Stryer L. Biochemistry. 7th ed. New York: W.H. Freeman; 2012.
-
36. Hammarström P, Carlsson U. Is the unfolded state the Rosetta Stone of the protein folding problem? Biochem Biophys Res Commun. 2000;276(2):393-398.[DOI]
-
37. Fersht AR. Nucleation mechanisms in protein folding. Curr Opin Struct Biol. 1997;7(1):3-9.[DOI]
-
38. He X, Zhu T, Wang X, Liu J, Zhang JZH. Fragment quantum mechanical calculation of proteins and its applications. Acc Chem Res. 2014;47(9):2748-2757.[DOI]
-
39. Kim S, Chen J, Cheng T, Gindulyte A, He J, He S, et al. PubChem 2023 update. Nucleic Acids Res. 2023;51(D1):D1373-D1380.[DOI]
-
40. Martínez L, Andrade R, Birgin EG, Martínez JM. PACKMOL: a package for building initial configurations for molecular dynamics simulations. J Comput Chem. 2009;30(13):2157-2164.[DOI]
-
41. VASP. Vienna Ab initio Simulation Package [Internet]. Available from: https://www.vasp.at/
-
42. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77(18):3865-3868.[DOI]
-
43. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B. 1999;59(3):1758.[DOI]
-
44. Ching WY, Poudel L, San S, Baral K. Interfacial Interaction between suolunite crystal and silica binding peptide for novel bioinspired cement. ACS Comb Sci. 2019;21(12):794-804.[DOI]
-
45. Adhikari P, Li N, Rulis P, Ching WY. Deformation behavior of an amorphous zeolitic imidazolate framework - from a supersoft material to a complex organometallic alloy. Phys Chem Chem Phys. 2018;20(46):29001-29011.[DOI]
-
46. San S, Li N, Tao Y, Zhang W, Ching WY. Understanding the atomic and electronic origin of mechanical property in thaumasite and ettringite mineral crystals. J Am Ceram Soc. 2018;101(11):5177-5187.[DOI]
-
47. Baral K, Adhikari P, Ching WY. Ab initio modeling of the electronic structures and physical properties of a-Si1-xGexO2 Glass (x= 0 to 1). J Am Ceram Soc. 2016;99(11):3677-3684.[DOI]
-
48. Adhikari P, Shafei L, San S, Rulis P, Ching WY. Origin of the existence of inter-granular glassy films in β-Si3N4. J Am Ceram Soc. 2020;103(2):737-743.[DOI]
-
49. Nielsen O, Martin RM. First-principles calculation of stress. Phys Rev Lett. 1983;50(9):697.[DOI]
-
50. Yao H, Ouyang L, Ching WY. Ab initio calculation of elastic constants of ceramic crystals. J Am Ceram Soc. 2007;90(10):3194-3204.[DOI]
-
51. Voigt W. Lehrbuch der kristallphysik (mit ausschluss der kristalloptik). bg teubner, jw edwards ed. leipzig berlin. Ann Arbor, Mich, 1928.
-
52. Reuß A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J Appl Math Mech. 1929;9(1):49-58.[DOI]
-
53. Hill R. The elastic behaviour of a crystalline aggregate. Proc Phys Soc A. 1952;65(5):349.[DOI]
-
54. Papadopoulou A, Laucks J, Tibbits S. Auxetic materials in design and architecture. Nat Rev Mater. 2017;2:17078.[DOI]
-
55. Stavroulakis GE. Auxetic behaviour: appearance and engineering applications. Phys Status Solidi B. 2005;242(3):710-720.[DOI]
-
56. Mott P, Roland C. Limits to poisson's ratio in isotropic materials. Phys Rev B. 2009;80(13):132104.[DOI]
-
57. Javanmardi Y, Colin-York H, Szita N, Fritzsche M, Moeendarbary E. Quantifying cell-generated forces: poisson's ratio matters. Commun Phys. 2021;4:237.[DOI]
-
58. Tilleman TR, Tilleman MM, Neumann MHA. The elastic properties of cancerous skin: Poisson's ratio and Young's modulus. Isr Med Assoc J. 2004;6(12):753-755.[PubMed]
-
59. AZoM. Properties of steel alloys [Internet]. Available from: https://www.azom.com/properties.Article
-
60. Helmenstine AM. Bulk modulus: definition and examples [Internet]. Available from: https://www.thoughtco.com/bulk-modulus-definition-and-examples
-
61. Hoek E, Bray J. Rock slope engineering. 3rd ed. London: CRC Press; 2014.[DOI]
-
62. Pariseau WG. Design and analysis in rock mechanics. 3rd ed. London: CRC Press; 2017.[DOI]
-
63. Wikipedia. Shear modulus [Internet]. Available from: https://en.wikipedia.org/wiki/Shear_modulus
-
64. Spanos P. Cure system effect on low temperature dynamic shear modulus of natural rubber. In: 2001 Technical Meeting of the American Chemical Society; Rubber Division. 2001.
-
65. Composite Panel Association. Medium density fiberboard (MDF) [Internet]. Leesburg (VA): Composite Panel Association [cited 2023 March 10]. Available from: https://www.compositepanel.org/products
-
67. Tian Y, Xu B, Zhao Z. Microscopic theory of hardness and design of novel superhard crystals. Int J Refract Met Hard Mater. 2012;33:93-106.[DOI]
-
68. Adhikari P, Wen A, French R, Parsegian VA, Steinmetz NF, Podgornik R, et al. Electronic structure, dielectric response, and surface charge distribution of RGD (1FUV) peptide. Sci Rep. 2014;4:5605.[DOI]
-
70. Adhikari P, Ching WY. Amino acid interacting network in the receptor-binding domain of SARS-CoV-2 spike protein. RSC adv. 2020;10(65):39831-39841.[DOI]
-
71. Ching WY, Rulis P. Historical account of the LCAO method. In: Electronic structure methods for complex materials. Oxford: Oxford University Press; 2012. p. 6-13.[DOI]
Copyright
© The Author(s) 2023. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Publisher’s Note
Share And Cite




