1. Introduction

The advent of moiré superlattices and twisted two-dimensional (2D) materials has opened new frontiers in condensed matter physics^[1-3], giving rise to the rapidly growing field of twistronics^[4-7]. By introducing a relative twist between two periodic structures, it is possible to engineer emergent quasiperiodic potentials and flat electronic bands, enabling exotic quantum phenomena such as superconductivity and correlated insulating states^[8-11]. Inspired by these developments, twisted photonic lattices have been proposed as an optical analogue, offering a tunable platform for manipulating light-matter interactions and realizing moiré-induced photonic phenomena, including, localization-delocalization transitions^[12], reconfigurable lasing^[13], linear and nonlinear beam shaping^[14,15], band flattening^[16], and topological transport^[17,18].

Non-Hermitian physics, describing open systems with gain and loss^[19], has attracted significant attention in photonics for its ability to produce unconventional optical effects such as parity-time (PT) symmetry breaking^[20], exceptional points^[21,22], and non-reciprocal light propagation^[23]. In photonics, introducing gain or loss is a common approach to study non-Hermitian effects, and has been extensively explored in conventional photonic lattices^[24-28]. Recent theoretical works suggest that combining moiré engineering with non-Hermitian modulation could introduce novel band topology and localization behavior beyond Hermitian systems^[29-32]. However, an experimental realization of a non-Hermitian twisted photonic lattice with active tunability has yet to be demonstrated. Atomic systems provide an ideal platform for such exploration due to their intrinsic coherence and flexibility^[33-35]. Multilevel configurations allow precise control of refractive index profiles, enabling the introduction of spatially structured gain and loss through optical fields, making them an excellent platform for tunable non-Hermitian photonic lattices^[36-39]. Using coherent atomic ensembles to couple non-Hermitian effects with lattice geometry in tunable twisted photonic lattices is expected to unlock new ways of controlling light beyond conventional systems.

In this work, we report a reconfigurable twisted photonic lattice with dynamically tunable non-Hermiticity. The lattice is realized in a four-level N-type atomic system by two superimposed incoherent stripe fields under an electromagnetically induced transparency (EIT) condition. These two incoherent stripe fields have the same period but different horizontal transmission, thereby generating a moiré-like pattern. Depending on the single-stripe-field parameters (frequency and power), the twisted photonic lattice exhibits different gain-loss rates, which induce a local flat band and lead to the directional localization of light in momentum space. By adjusting the twist angle, the localization direction can be dynamically steered without affecting the underlying non-Hermiticity. Different from Hermitian moiré flat-band scenarios mainly driven by geometric bandwidth folding and compression^[40,41], our flat band is locally induced by gain-loss modulation when non-Hermiticity becomes comparable to the moiré-reduced inter-branch coupling near high-symmetry points. The synergistic effect of non-Hermiticity and lattice geometric twisting provides a flexible platform for investigating light control in non-Hermitian photonic lattices and their device applications^[42,43].

2. Methods

Figure 1A illustrates the experimental configuration for realizing a non-Hermitian twisted photonic lattice inside a vapor cell. The lattice is optically induced by the superposition of a pump and a control field, which are modulated by a spatial light modulator into stripe patterns with an identical period of 200 μm. The pump beam is aligned along the x-axis, while the control beam is rotated by a twist angle θ, forming a two-dimensional moiré-like structure. A weak Gaussian signal field is in oblique incidence into the vapor to excite the specific band structure, and forms a four-level N-type atomic configuration together with the two fields under EIT, as illustrated in Figure 1B. In this configuration, the signal (wavelength λ_s = 795 nm, Rabi frequency Ω_s, and frequency detuning Δ_s) and control (wavelength λ_c = 795 nm, Rabi frequency Ω_c, and frequency detuning Δ_c) fields respectively excite atoms from the ground state |1〉(|5S_1/2, F = 2〉) and |2〉(|5S_1/2, F = 3〉) to the excited state |3〉(|5P_1/2, F = 2〉), while the pump (wavelength λ_p = 780 nm, Rabi frequency Ω_p, and frequency detuning Δ_p) field connects the transition |1〉→ |4〉(|5P_3/2, F = 3〉). The output signal in momentum space, imaged by a Fourier lens and captured in real time by a charge-coupled device (CCD), reveals the properties of the twisted photonic lattice.

Display Full Size

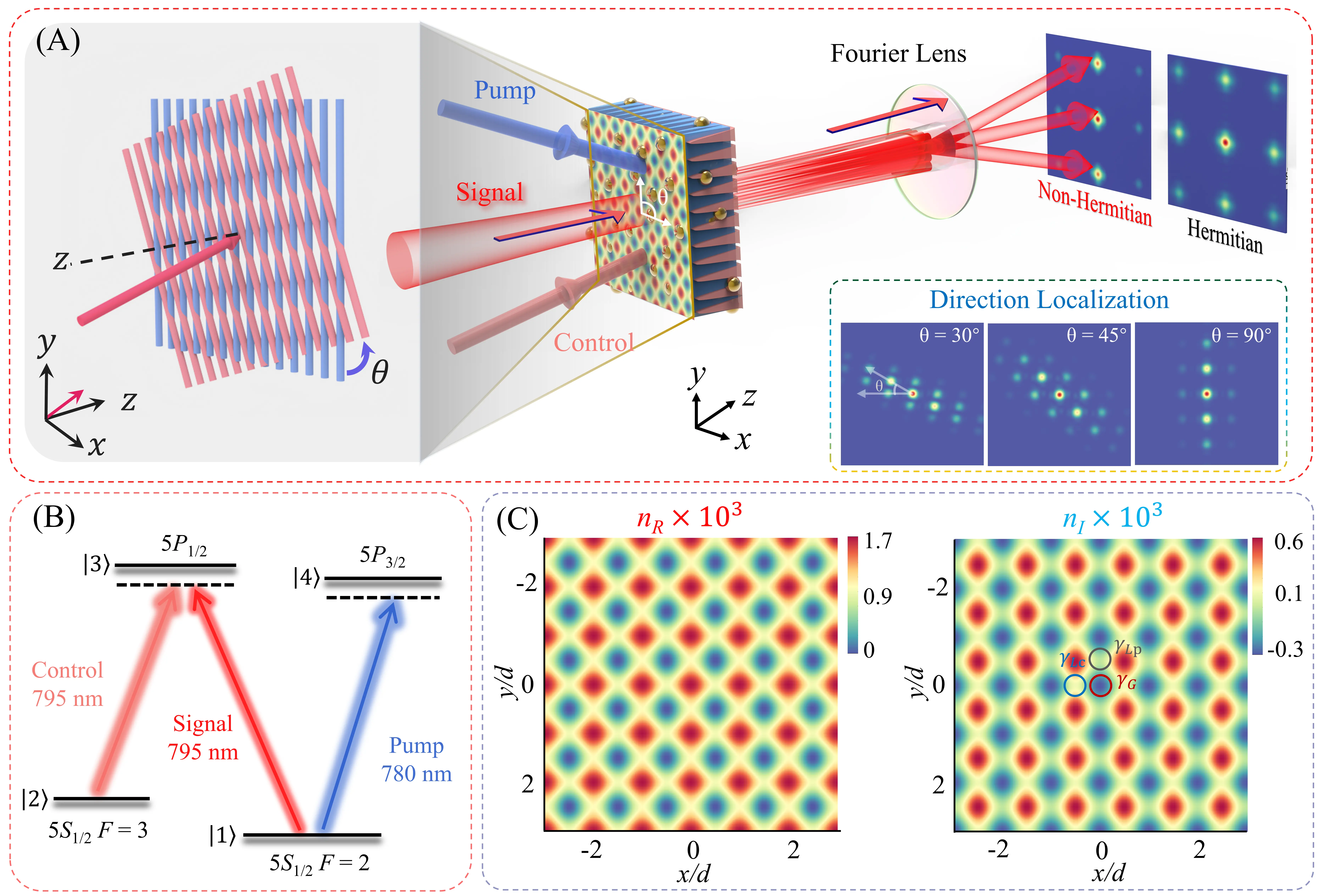
Figure 1. Realization of non-Hermitian twisted photonic lattice. (A) Schematic diagram; (B) Four-level N-type ⁸⁵Rb atomic energy-level diagram; (C) The real and imaginary parts of the refractive index. Here, θ = 90°, Δ_s = -2π × 15 MHz, Δ_c = -2π × 21.5 MHz, Δ_p = 2π × 6 MHz, Ω_s = 2π × 0.1 MHz, Ω_c = 2π × 4.8 MHz, Ω_p = 2π × 2.5 MHz, and d ≈ 200 μm is the spatial period of the stripe fields.

3. Results and Discussion

3.1 Theoretical simulation of non-Hermitian twisted photonic lattice

The propagation behavior of the signal field through the lattice is governed by the paraxial Schrödinger-like equation^[44]:

(1)$i\frac{\partial \Psi (x,y,z)}{\partial z}=\frac{1}{2k_0}{\nabla }^2\Psi (x,y,z)-\frac{k_0\Delta n(x,y)}{n_0}\Psi (x,y,z)$

where $\Psi (x,y,z)$ represents the envelope of the signal field, k₀ is the wavenumber, n₀ ≈ 1 is the background refractive index, and Δn = n - n₀ is the change of the refractive index. The complex refractive index of the twisted photonic lattice, strongly correlated with systemic susceptibility, is expressed as n = n₀ + n_R + in_I, where n_R and n_I are the real (dispersion) and imaginary (gain/loss) parts of the refractive index, respectively (Supplementary materials).

The calculated n_R and n_I are shown in Figure 1C, respectively, with θ = 90° for clearer illustration. The n_R map clearly depicts the light distribution from the two superimposed stripe fields, which shows that strong points form in the overlapping region while the non-overlapping parts maintain their original distribution due to the absence of interference. Compared with the two three-level structures (V- and λ-type), the four-level N-type structure can induce Raman gain on the signal field^[45]. This N-type configuration enables independent and flexible control of gain-loss effects and twisted lattice fields, which is not readily achievable in simpler two- or three-level systems. As a result, overlapping regions exhibit gain (γ_G) since n_I < 0, while non-overlapping parts retain loss (γ_Lp and γ_Lc) since n_I > 0, establishing a non-Hermitian twisted photonic lattice with staggered gain and loss (Supplementary materials).

By tuning system parameters, the relative contributions of gain and loss can be dynamically controlled, enabling in-situ modulation of non-Hermiticity. Figure 2A shows n_R and n_I of the gain points at different control field frequency detuning Δ_c with a fixed Δ_s = -2π × 15 MHz and Δ_p = 2π × 6 MHz. As the red-detuned control field frequency gradually decreases (from -2π × 26 MHz to -2π × 18 MHz), the γ_G in the overlapping region (or |n_I|) first increases and then decreases, with the maximum occurring at -2π × 20 MHz. Meanwhile, the n_R decreases nearly monotonically during this process. This results in the system’s non-Hermiticity (defined as |n_I/n_R| in the overlapping point^[46]) reaching its maximum near -2π × 20 MHz, as shown in Figure 2B.

Display Full Size

Figure 2. Band structure evolution induced by non-Hermiticity. (A) The real and imaginary parts of the gain points under different Δ_c; (B) The evolution of systemic non-Hermiticity, defined as |n_I/n_R| in (A); (C-E) Band structures along the high symmetry lines. The illustrations show the imaginary parts of the band structures around the M point, where bands 2 and 3 experience the same loss and therefore overlap in the imaginary spectrum; (C1-E1) field distribution at M, and (C2-E2) spatial distribution in momentum space. Here, Δ_c = -2π × 23 MHz in (C), Δ_c = -2π × 21.5 MHz in (D), and Δ_c = -2π × 20 MHz in (E). The other parameters are the same as those in Figure 1.

The non-Hermitian effect usually accompanies the transformation of the eigenvalue spectra to complex values, enabling non-Hermitian phenomena analogous to the PT-symmetry breaking transition^[47]. The energy band of such continuous-tunable system can be effectively calculated by the plane-wave expansion method^[48]. By substituting $\Psi (x,y,z)$ = φ_k (x,y)e^iβ(k)z into Eq. (1), φ_k (x,y) obeys the following:

(2)$\beta \left(k\right){\phi }_k(x,y)=\frac{1}{2k_0}\frac{{\partial }^2{\phi }_k(x,y)}{\partial x^2}+\frac{1}{2k_0}\frac{{\partial }^2{\phi }_k(x,y)}{\partial y^2}-\frac{k_0\Delta n(x,y)}{n_0}{\phi }_k(x,y)$

where φ_k (x,y) is the Bloch mode and β(k) corresponds to the propagation constant.

Figure 2C, D, and E shows the corresponding band structure along the high-symmetry line. At Δ_c = -2π × 23 MHz, a point degeneracy appears at M and small gaps emerge between band 1 and band 2 in Re[β] from X to M, accompanied by smaller values in Im[β]. The momentum-space intensity distribution (Figure 2C2), obtained via 2D Fourier transform of the field distribution at M (Figure 2C1), reveals stronger first-order diffraction along the x-axis than the y-axis. As Δ_c increases to -2π × 21.5 MHz (Figure 2D), band 1 and band 2 in Re[β] completely overlap from X to M, while Im[β] remains nearly unchanged. Correspondingly, the momentum-space intensity distribution in the x- and y-axis become comparable (Figure 2D2). At Δ_c = -2π × 20 MHz, near maximum non-Hermiticity, the increased Im[β] transforms the point degeneracy into a local flat band around M in Re[β] (Figure 2E). This flat band corresponds to regions of near-zero group velocity^[38], which trap optical modes in momentum space and serve as the origin of directional localization^[49,50]. The corresponding momentum-space intensity distribution (Figure 2E2) confirms this behavior, showing energy concentration along the y-axis rather than being evenly distributed. These results show that the flat band is parameter dependent and originates from gain-loss-induced spectral flattening, thereby establishing a clear link between the momentum-resolved diffraction patterns and the underlying non-Hermitian photonic band structure.

To make the origin of the local flat band near M explicit, we employ a minimal two-mode non-Hermitian model for the two nearly degenerate folded branches that dominate the local dispersion:

(3)$H_{eff}\left(k\right)=\left(\begin{array}{cc}{\beta }_0\left(k\right)-i{\gamma }_G\left({\Delta }_c\right)& J(k,\theta )\\ J^{\ast }(k,\theta )& {\beta }_0\left(k\right)+i{\gamma }_L\left({\Delta }_c\right)\end{array}\right)$

giving ${\beta }_{\pm }={\beta }_0+\frac{i}{2}({\gamma }_L-{\gamma }_G)\pm \sqrt{|J{|}^2-{\Gamma }^2}$, where J is the moiré-renormalized inter-branch coupling (tuned by the twist angle θ), γ_L ≈ γ_LP in our regime since γ_LC « γ_LP, and Γ = (γ_G + γ_L)/2. Near M, the moiré geometry makes |J| small and weakly k-dependent; thus increasing Γ suppresses the splitting and flattens Re[β] locally, consistent with Figure 2C, D, and E.

3.2 Experimental control of non-Hermitian-induced directional localization

Figure 3 shows the experimental configuration for implementing a non-Hermitian twisted photonic lattice in a rubidium vapor cell. The pump and control fields, emitted from two independent tapered-amplified diode lasers (TA pro, Toptica), and frequency shifted by a pair of frequency shift modules (FSM, a double-pass configuration based on the acoustic optical modulator), are first expanded by the beam expanders, and then incident into the left and right half of the screen in a phase-controlled spatial light modulator (SLM, Hamamatsu), respectively. The output pump and control fields are filtered by the 4f filter system, consisting of the focal length 200 mm lens and a spatial filter, to select the stripe fields. By loading appropriate phase patterns onto the SLM, we can control the geometry of the photonic lattice via twist angle θ between the two spatial stripe fields. The weak Gaussian signal beam, generated by the external cavity diode laser (DL pro, Toptica), and frequency shifted by an FSM, is in oblique incidence through the twisted photonic lattice inside the atomic vapor. The output signal beam is observed in momentum space under two partially overlapped EIT conditions and recorded by a CCD in real time. The ⁸⁵Rb vapor cell has a diameter and length of 2.5 cm, with its temperature controlled at ~373 K, corresponding to an atomic density of ~6.01 × 10¹² cm^-3.

Display Full Size

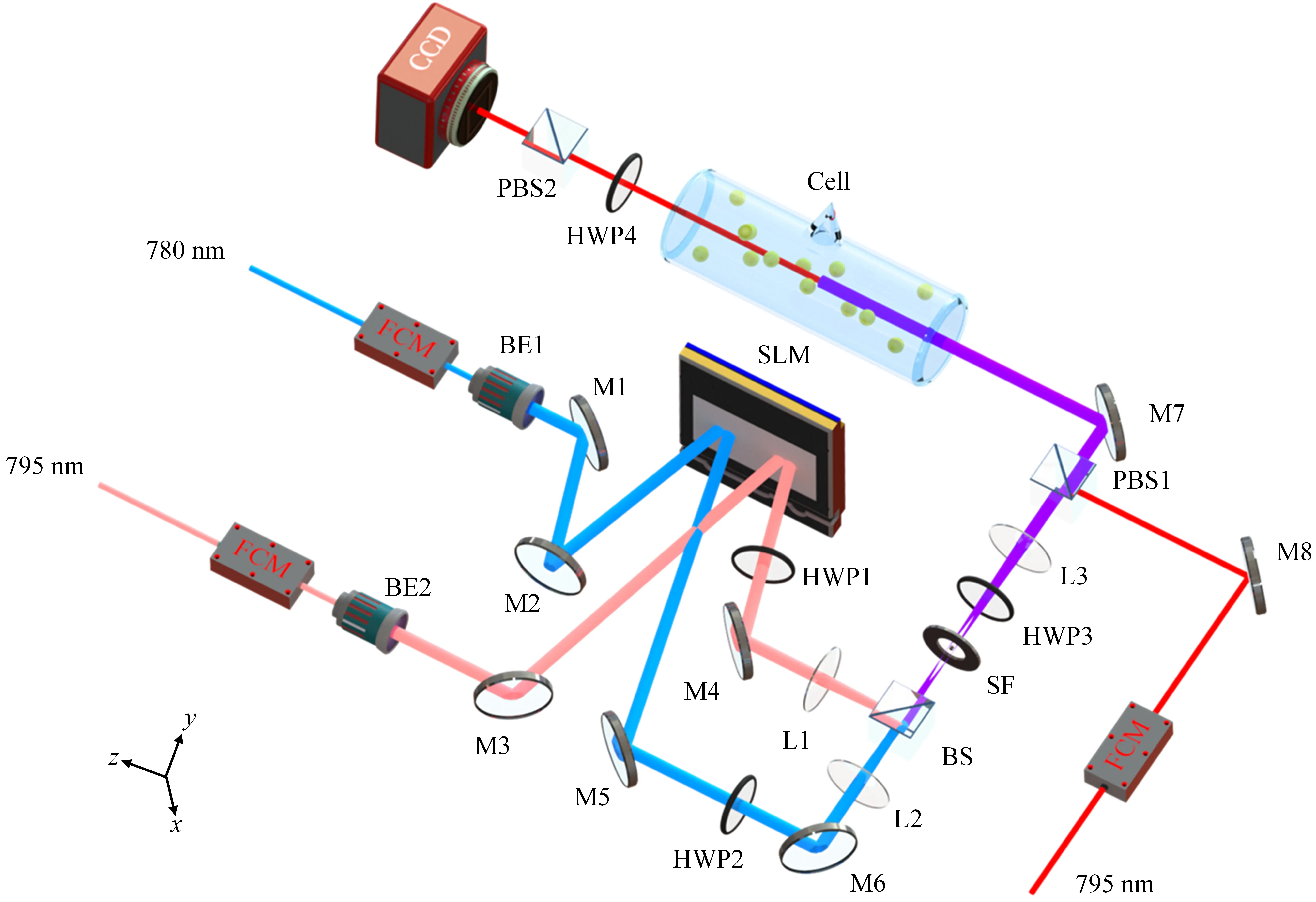
Figure 3. Experimental setup for non-Hermitian twisted photonic lattices. FSM, frequency shift module; BE: beam expander; M: high reflection mirror; SLM: spatial light modulator; HWP: half-wave plate; SF: spatial filter; L: lens; BS: beam splitter; PBS: polarization beam splitter; CCD: charge-coupled device.

Figure 4 presents the experimental confirmation of the non-Hermitian-driven transition from delocalization to directional localization under signal field oblique incidence. The momentum-space images in Figure 4A exhibit a progressive change from isotropic intensity (Δ_c = -140 MHz) to strong anisotropy at Δ_c = -120 MHz, where the signal field energy concentrates along one momentum axis. By extracting the intensity of first-order diffraction along x- and localization-axis (defend as I_x1 and I_θ1), respectively, the evolution of the delocalization to localization can be captured by the directional localization factor (DLF), defined by I_θ1/(I_x1 + I_θ1), which increases sharply beyond 0.5, signaling the onset of localization (Figure 4B). Such a transition is analogous to a PT-symmetry-breaking phase transition, where non-Hermiticity increases and dominates the system dynamics^[36].

Display Full Size

Figure 4. Detuning-driven transition from delocalization to directional localization. (A) Experimental observation of momentum-space images of signal field at different Δ_c; (B) Evolution of the directional localization factor and theoretical simulated gain-to-loss ratio with Δ_c. Here, the dashed line marks that the directional localization factor is equal to 0.5 (or the gain-loss effect reaches balance), introduced to guide the eye and to quantify the onset of directional localization. The theoretical parameters are same as in Figure 1. The experimental parameters are Δ_s = -90 MHz, Δ_p = 40 MHz, and θ = 90°, with the powers of the control, pump, and signal fields being P_c = 45 mW, P_p = 25 mW, and P_s = 5 mW, respectively.

Non-Hermitian directional localization arises from the introduction of gain and loss in the lattice. In the selected Δ_c range, the loss term γ_Lc, which is influenced by Δ_c, remains much smaller than γ_Lp (Supplementary materials). Therefore, the DLF is primarily governed by the ratio γ_G/γ_Lp, i.e., the gain-to-loss ratio. As shown in Figure 4B, this ratio exceeds unity within the same Δ_c range where the DLF is beyond 0.5, confirming that the lattice enters a balanced or gain-dominated regime necessary for non-Hermitian localization. Notably, the Δ_c value corresponding to maximum DLF aligns with the parameter regime where Figure 2 predicts the emergence of a local flat band, validating the connection between experimental momentum-space observations and theoretical band calculations. At smaller detuning (Δ_c > -120 MHz), the localization weakens as the gain-loss modulation deteriorates, restoring partial isotropy in the pattern. This controlled transition demonstrates the feasibility of dynamically tuning non-Hermitian effects to engineer directional light confinement in momentum space.

While Figure 2 and Figure 4 establish the role of non-Hermiticity in driving localization, Figure 5 demonstrates that the direction of localization can be actively controlled by tuning the lattice twist angle θ. The schematic of the lattice with a twist angle is shown in Figure 5A. For a different twist angle, i.e., θ = 30° shown in Figure 5B, the calculated n_R and n_I remain essentially unchanged compared to those in Figure 1C, indicating that the twist does not alter the underlying non-Hermiticity. The corresponding momentum-space images exhibit strong directional localization similar to that observed at θ = 90° (Figure 5C), but with the localized axis rotated according to the imposed twist (Supplementary materials). This behavior is consistent with the reciprocal-lattice rotation induced by twisting^[51], which reorients the momentum channels associated with flat-band states (Supplementary materials).

Display Full Size

Figure 5. Twist-angle control of localization direction. (A) Schematic of the non-Hermitian twisted photonic lattice with θ; (B) Simulated real and imaginary parts of the refractive index at θ = 30°; (C) Evolution of the directional localization factor at different θ as a function of Δ_c. The dashed lines are consistent with Figure 4B; (D) Experimental observation of momentum-space images under different θ, here, Δ_c = -120 MHz. The other theoretical and experimental parameters are the same as in Figure 1 and Figure 4A, respectively.

Figure 5D further confirms that the localization axis scales with θ, allowing continuous and reversible control of light propagation direction. Importantly, under non-twisted conditions (θ = 0), the diffraction remains symmetric, underscoring the necessity of geometric twist for directional control. These results reveal a unique degree of freedom-lattice twist-that synergizes with non-Hermiticity to enable dynamic, reversible, and angle-dependent manipulation of light localization in 2D photonic systems.

In addition to detuning and twist angle, the degree of non-Hermiticity can be tuned by varying the control beam power, as shown in Figure 6. Increasing the control power from 5 mW to 45 mW significantly enhances the depth of the refractive index modulation and the gain-loss ratio, as reflected in the evolution of momentum-space images (Figure 6A). At low power (5 mW), the pattern remains nearly isotropic with a low DLF (< 0.1), corresponding to a weakly non-Hermitian regime. As the power reaches 15 mW, the DLF approaches 0.5, indicating a critical point for the transition from delocalization to localization. Strong directional localization is observed when the control power is increased to 45 mW, raising the DLF to around 0.8 (Figure 6B). These observations confirm that the non-Hermitian phase transition and directional localization can be controlled through multiple experimental knobs, including frequency detuning, lattice twist, and optical power. This tunability underscores the versatility of the platform for dynamic light control and suggests pathways toward implementing reconfigurable non-Hermitian photonic devices.

Display Full Size

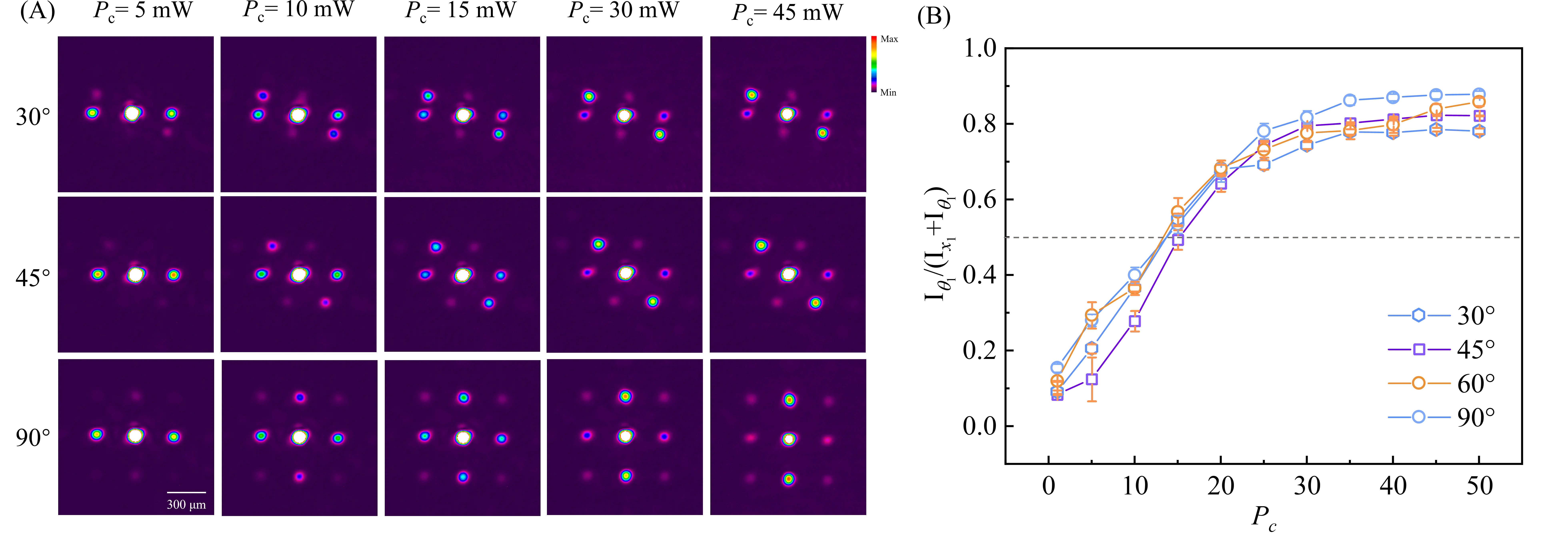
Figure 6. Power-dependent tuning of localization strength. (A) Experimental observation of momentum-space images recorded at different control beam powers for θ = 30°, 45° and 90°, respectively; (B) Evolution of the directional localization factor as a function of control beam power for θ = 30°, 45°, 60° and 90°, respectively. The other theoretical and experimental parameters are the same as in Figure 1 and Figure 4D, respectively.

4. Conclusion

In summary, we have experimentally realized a non-Hermitian twisted photonic lattice with controllable gain-loss modulation and demonstrated a dynamic transition from delocalization to directional localization in momentum space. This transition originates from the emergence of local flat bands in the non-Hermitian band structure, which suppress the group velocity and confine optical modes along specific momentum channels. By tuning system parameters, including laser frequency detuning, lattice twist angle, and laser power, we achieved real-time control over both the degree and direction of localization. These results establish a direct link between momentum-space imaging and non-Hermitian band reconstruction and reveal a powerful strategy for manipulating light through the synergy of geometric twist and non-Hermiticity. The demonstrated flexibility provides a promising platform for designing reconfigurable photonic devices, such as non-Hermitian beam routers, optical switches, and flat-band-based light confinement components^[42,43].

Supplementary materials

The supplementary material for this article is available at: Supplementary materials.

Authors contribution

Yuan J, Niu F, Zhang H, Wu C: Conceptualization, methodology, investigation, formal analysis, data curation, writing-review & editing.

Chen G, Wang L, Xiao L, Jia S: Supervision, formal analysis, data curation, writing-review & editing.

Conflicts of interest

Gang Chen is an Editorial Board Member of Light Manipulation and Applications. The other authors declare no conflicts of interest.

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and materials

Data supporting the findings of this study are available from the corresponding author upon reasonable request.

Funding

This work is supported by the Innovation Program for Quantum Science and Technology (2023ZD0300902); the National Key R&D Program of China (2022YFA1404500); the National Natural Science Foundation of China (12474359, 62475136); the Fundamental Research Program of Shanxi Province (202403021211158); and the Fund for Shanxi “1331 Project” (This program does not have a grant number).

Copyright

© The Author(s) 2026.