1. Introduction

Rattling vibrations, which are large-amplitude, localized oscillations of weakly bound atoms, have emerged as a powerful mechanism for suppressing lattice thermal conductivity κ_L in thermoelectric materials. By disrupting long-range phonon propagation, rattling modes enhance phonon-phonon scattering and induce glass-like thermal transport in otherwise crystalline solids^[1,2]. Key signatures of rattling include avoided crossings between acoustic and optical phonon branches, large atomic displacement parameters, and flat, low-frequency vibrational modes^[3,6]. Recent high-throughput screening has further revealed that loosely bonded atoms, identified through simple geometric descriptors such as long bond lengths relative to covalent radii, can reliably indicate rattling behavior, underscoring the statistical robustness and generality of rattling as a design principle for low thermal conductivity^[7].

Among the materials exhibiting rattling-induced phonon scattering, full-Heusler compounds with the general formula X₂YZ have recently attracted attention for their thermoelectric potential^[8-11]. These intermetallics combine semimetallic or narrow-gap electronic structures with the possibility of incorporating heavy, weakly bonded elements in a highly symmetric cubic lattice. In analogy to clathrates and skutterudites^[4,12,13], full-Heuslers can host internal “rattlers” that strongly reshape phonon dispersions and scattering pathways, yet the mechanisms underlying their heat transport remain less explored.

Traditional analyses based on the Peierls-Boltzmann transport equation (BTE) attribute thermal resistance to three-phonon (3ph) scattering^[14]. However, recent studies have shown that in systems with pronounced rattling behavior and flat phonon bands, four-phonon (4ph) scattering^[8,15-18] and wave-like, coherent phonon transport^[2,19-21] can play critical roles. This renders BTE approaches insufficient and necessitates the frameworks such as the Wigner transport equation to capture phase-coherent heat flow.

While rattling phenomena have been widely investigated in skutterudites, clathrates, and Zintl phases, the role of metallic rattling bonds in full-Heusler compounds, as well as their distinct impact on phonon dispersion and scattering, remains less explored. Moreover, a quantitative and tunable link between rattling strength, band flatness, and multiphonon scattering within a single material system is still lacking. Additionally, how rattling modes selectively enhance both particle-like scattering and wave-like coherence in a frequency-resolved manner requires further clarification.

In this work, we address these gaps by investigating the full-Heusler compound Sr₂HgSn as a model system. Using first-principles lattice dynamics combined with force-constant modulation and Wigner transport analysis, we reveal a tunable, frequency-selective crossover between κ_P and κ_c driven by Hg rattling. Our work introduces a quantitative flatness descriptor, correlates rattling strength with 3ph/4ph scattering phase spaces, and demonstrates that metallic rattling in a high-symmetry cubic lattice can simultaneously suppress κ_P and enhance κ_c, offering a distinct platform for phonon engineering beyond conventional cage-like structures. These findings advance the understanding of rattling-mediated thermal transport and provide new design strategies for tuning both scattering and coherence in thermoelectric materials.

2. Numerical Methods

The calculations are performed using the Vienna Ab Initio Simulation Package based on density functional theory^[22], employing the projector augmented wave method with the PBEsol exchange-correlation functional (a revised Perdew-Burke-Ernzerhof generalized gradient approximation for solids)^[23]. A plane-wave cutoff energy of 500 eV is used. Atomic positions are optimized with an energy convergence criterion of 10^-5 eV between consecutive steps and a maximum Hellmann-Feynman force tolerance of 10^-3 eV/Å. The primitive cell was optimized using a Γ-centered q-mesh of 13 × 13 × 13 in the Brillouin zone.

For the ab initio molecular dynamics (AIMD) simulations, the 3 × 3 × 3 supercell was constructed by expanding the primitive cell with Γ-centered 1 × 1 × 1 k-mesh. The simulations run for 30 ps with a 1 fs timestep. Interatomic force constants (IFCs) are extracted from AIMD trajectories using the temperature-dependent effective potential method^[24]. Cutoff radii for third-order and fourth-order IFCs are set to 6 Å. The lattice thermal conductivity (κ_L) and related parameters, including phonon relaxation times, are computed using the ShengBTE software^[25,26], which implements an iterative solution scheme. A q-mesh of 13 × 13 × 13 is adopted in the first irreducible Brillouin zone, with a Gaussian smearing width of 0.2. The 4ph scattering rate is efficiently calculated using a maximum likelihood estimation method^[27] with a sample size of 4 × 10⁵.

3. Results and Discussion

As a full-Heusler compound with stoichiometry X₂YZ (space group $\mathrm{Fm}\bar{3}m$), Sr₂HgSn crystallizes in a cubic structure, as illustrated in Figure 1a, where Sr, Hg, and Sn occupy the 8c, 4a, and 4b Wyckoff positions, respectively. The lattice constant is 7.94 Å, with Sr-Sn/Hg and Hg-Sn bond lengths of 3.44 Å and 3.97 Å, respectively. To evaluate the bonding strength, we compute the second-order interatomic force constants, as shown in Figure 1b. The nearest-neighbor Sr-Sn, Sr-Hg, and Hg-Sn force constants are 0.97, 0.61, and 0.10 eV/Ų, respectively, indicating that Hg interacts weakly with its surrounding atoms. The exceptionally low force constant 0.10 eV/Ų and long bond length (3.97 Å) between Hg and Sn suggest a highly delocalized metallic interaction. This bonding environment creates a rattling model scenario, in which the weakly bonded Hg atoms behave as rattling guests within the more strongly coupled Sr₂Sn framework. This is further confirmed by the electron localization function (ELF) analysis in Figure 1c. The ELF ranges from 0 to 1, where 1 signifies complete electron localization, 0 indicates full delocalization, and 0.5 represents an electron-gas-like pair distribution. The ELF value of approximately 0.5 along the Hg-Sn bond path clearly indicates the presence of a weak but characteristic metallic bond, while the nearly zero ELF between Sr and Sn/Hg confirms ionic bonding. The Bader effective charges further support this interpretation, with Sr, Sn, and Hg carrying charges of +1.22, -1.55, and -0.89, respectively. The similar bond lengths but smaller charge difference between Sr and Hg (compared to Sr and Sn) suggest weaker ionic bonding for the Sr-Hg pair, in agreement with Coulomb’s law.

Display Full Size

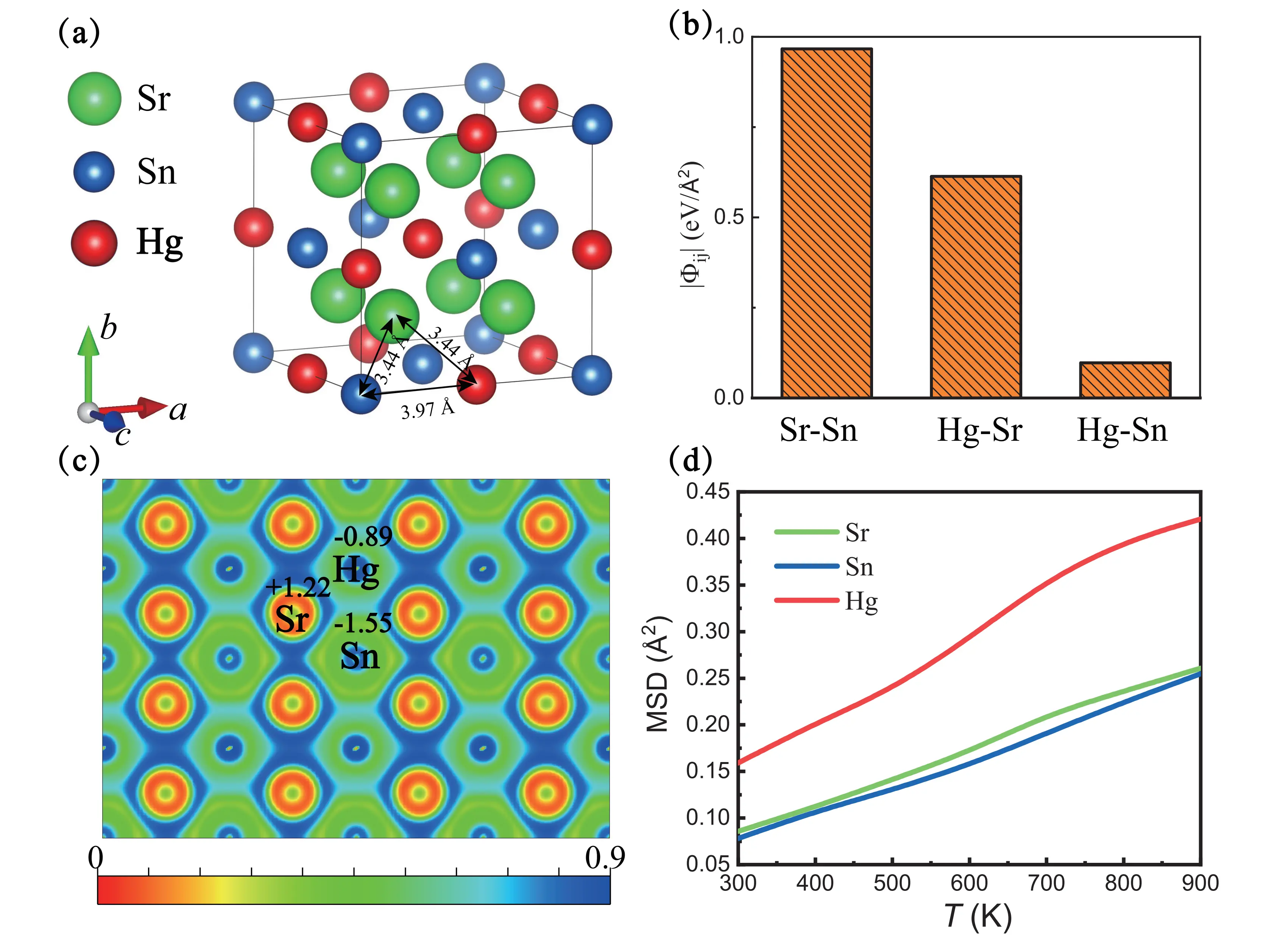
Figure 1. (a) Cubic crystal structure of full-Heusler Sr₂HgSn (space group Fm3m) with atomic positions; (b) Interatomic force constants showing bond strengths; (c) ELF and Bader charge analysis revealing the bonding nature; (d) Temperature-dependent atomic MSDs demonstrating lattice dynamics. ELF: electron localization function; MSDs: mean square displacements.

Figure 1d shows the temperature-dependent atomic mean square displacements (MSDs). The weak metallic bonding between Hg and Sn, combined with the overall weak interactions around Hg, results in significantly larger MSDs for Hg compared to Sr and Sn. This rattling-dominated lattice dynamics has important implications for the thermal transport properties discussed in the following sections.

As revealed in Figure 2a, the temperature-evolved phonon dispersion displays characteristic avoided-crossing features between acoustic and optical branches (dashed circles), where the low-frequency optical modes generated by weakly bonded Hg atoms interact with propagating acoustic modes. This dynamic coupling induces phonon branch repulsion while simultaneously exhibiting abnormal hardening with temperature - a fingerprint of rattling behavior where guest atoms oscillate in a weakly constrained potential^[5,28,29].

Display Full Size

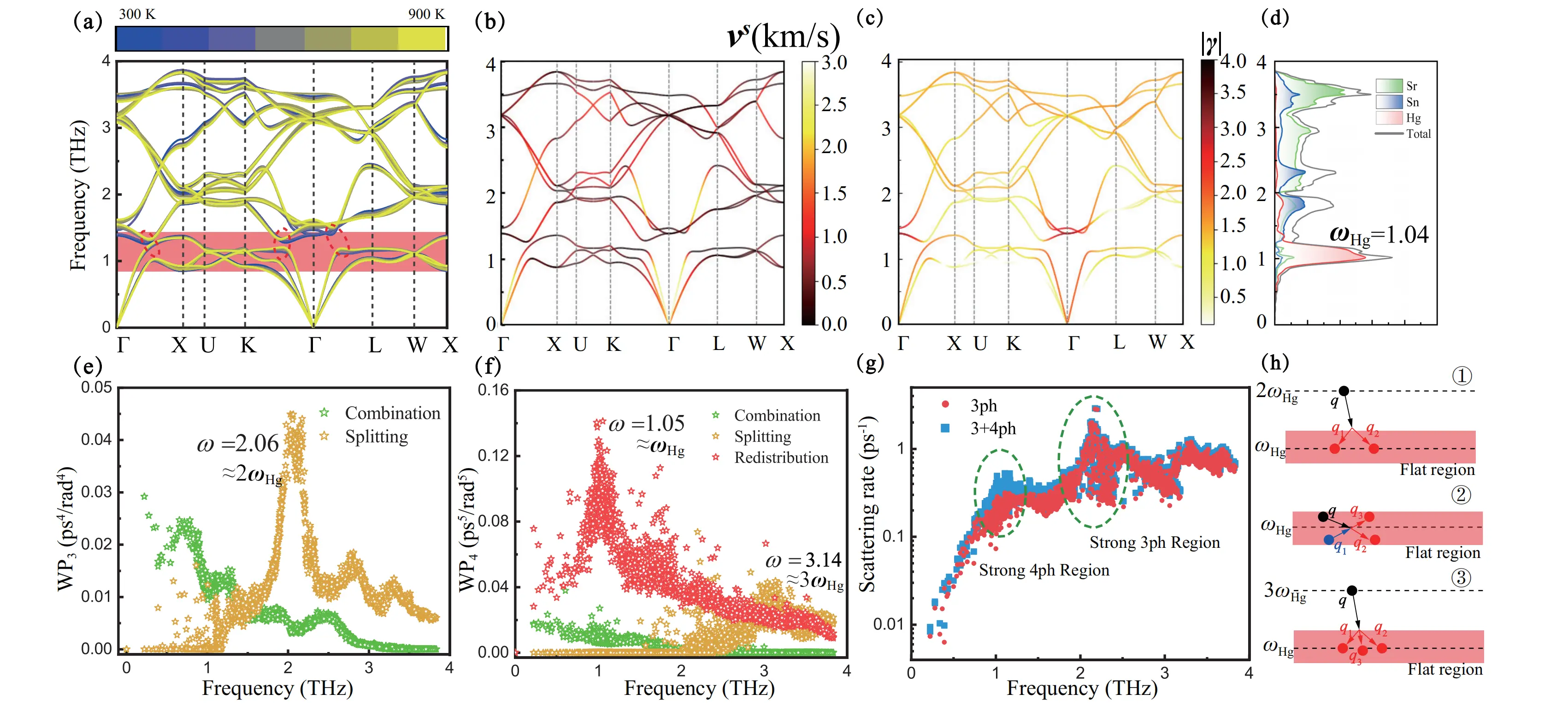
Figure 2. (a) Temperature-dependent phonon dispersion. Red rectangles mark flat phonon band regions and red dashed lines mark avoided crossings; (b) Group velocity-projected phonon dispersion; (c) Grüneisen parameter-projected phonon dispersion; (d) Atom-projected phonon density of states; (e) 3ph scattering phase space showing 2ω_Hg emission peak; (f) 4ph scattering phase space with ω_Hg redistribution peak and 3ω_Hg splitting peak; (g) Total phonon scattering rates with 3ph and processes; (h) Schematic of dominant scattering mechanisms.

The profound impact on thermal transport is quantified in Figure 2b, where group velocity projections expose dramatically flattened dispersions (< 0.5 km/s) near the avoided-crossing region. These sluggish phonon modes, visualized as near-horizontal bands, create intrinsic bottlenecks for heat propagation. Complementary anharmonicity analysis in Figure 2c reveals giant Grüneisen parameters (> 3) localized at the interaction zones, confirming the rattling mechanism generates exceptional bond stiffness variations during atomic vibrations.

The vibrational decomposition in Figure 2d reveals the unique nature of rattling dynamics: while the sharp, Hg-dominated peak at 1.04 THz indicates localized vibrations in momentum space (flat dispersion), the avoided-crossing in Figure 2a demonstrates their delocalized character in real space through hybridization with acoustic phonons. This dual behavior - localized in energy but extended in spatial influence - is a hallmark of rattling systems, where weakly bonded atoms maintain distinct vibrational signatures while strongly perturbing the host lattice dynamics.

The phonon scattering phase space analysis in Figure 2e,f reveals two characteristic peaks originating from the flat rattling modes at 1.04 THz (ω_Hg). Figure 2e shows a pronounced 3ph emission peak at 2ω_Hg, resulting from the decay process q → q₁ + q₂, where energy conservation requires ω_q = ω_q1 + ω_q2 ≈ 2ω_Hg while momentum selection is relaxed due to the flat dispersion of Hg-derived modes. This enables efficient decay of high-energy phonons into pairs of rattling modes^[14].

Similarly, Figure 2f exhibits a 4ph redistribution peak at ω_Hg from processes q + q₁ → q₂ + q₃ where the flat bands again facilitate momentum conservation^[17]. Moreover, a small 4ph splitting peak near 3ω_Hg from processes q → q₁ + q₂ + q₃ is observed. The combined scattering effects are quantified in Figure 2g, where the total scattering rate displays twin peaks with a lower-frequency peak near ω_Hg (strong 4ph) and a higher-frequency peak near 2ω_Hg (strong 3ph).

The microscopic scattering mechanisms are illustrated in Figure 2h, contrasting the 3ph emission (above) and 4ph redistribution (below) processes that dominate at their respective characteristic frequencies. The 3ph process shows a high-frequency phonon splitting into two rattling modes, while the 4ph process depicts the redistribution of phonon populations through collisions between rattling modes.

According to the Wigner transport equation, as derived from the Wigner phase-space formulation of quantum mechanics, the lattice thermal conductivity (κ_L) in complex crystals consists of two distinct contributions: the particle-like thermal conductivity (κ_P), describing propagating phonons, and the glass-like coherence term (κ_c), accounting for wave-like tunneling between phonon modes^[30-32].

The particle-like component κ_P is given by:

(1)${\kappa }_{p,\alpha \beta }=\frac{1}{V{N}_q}\sum _q{c}_q^s{v}_{q,\alpha }^s{v}_{q,\beta }^s{\tau }_q^s$

Where V is the volume of the primitive unit cell, and N_q represents the number of sampled q-points in the first Brillouin zone, $c_q^s$ is the mode-resolved heat capacity, $v_{q,\alpha }^s$ denotes the group velocity component along Cartesian direction α, and ${\tau }_q^s$ is the phonon lifetime of mode (q,s).

The glass-like contribution κ_c emerges from phonon mode interference:

(2)$\begin{array}{cc}{\kappa }_{c,\alpha \beta }=\frac{{ħ}^2}{k_B{T}^{2}V{N}_q}\sum _q\sum _{s\ne s^{\prime }}& \frac{{\omega }_q^s+{\omega }_q^{s^{\prime }}}{2}{v}_{q,\alpha }^{s,s^{\prime }}{v}_{q,\beta }^{s,s^{\prime }}\\ & \times \frac{{\omega }_q^s{n}_q^s(n_q^s+1)+{\omega }_q^{s^{\prime }}{n}_q^{s^{\prime }}(n_q^{s^{\prime }}+1)}{4{({\omega }_q^s-{\omega }_q^{s^{\prime }})}^2+{({\Gamma }_q^s+{\Gamma }_q^{s^{\prime }})}^2}({\Gamma }_q^s+{\Gamma }_q^{s^{\prime }})\end{array}$

Where h is the reduced Planck constant, κ_B the Boltzmann constant, $n_q^S={[e^{h\omega /k_{B}T}-1]}^{-1}$ the Bose-Einstein distribution, and ${\Gamma }_q^s=1/{\tau }_q^s$ the scattering rate.

Figure 3 reveals the distinct temperature dependence of thermal transport components. As shown in Figure 3a, κ_p exhibits a gradual decrease with rising temperature, dropping from 1.05 W/mK at 300 K (considering only 3ph scattering) to 0.88 W/mK when 4ph interactions are included, representing a 16% reduction.

Display Full Size

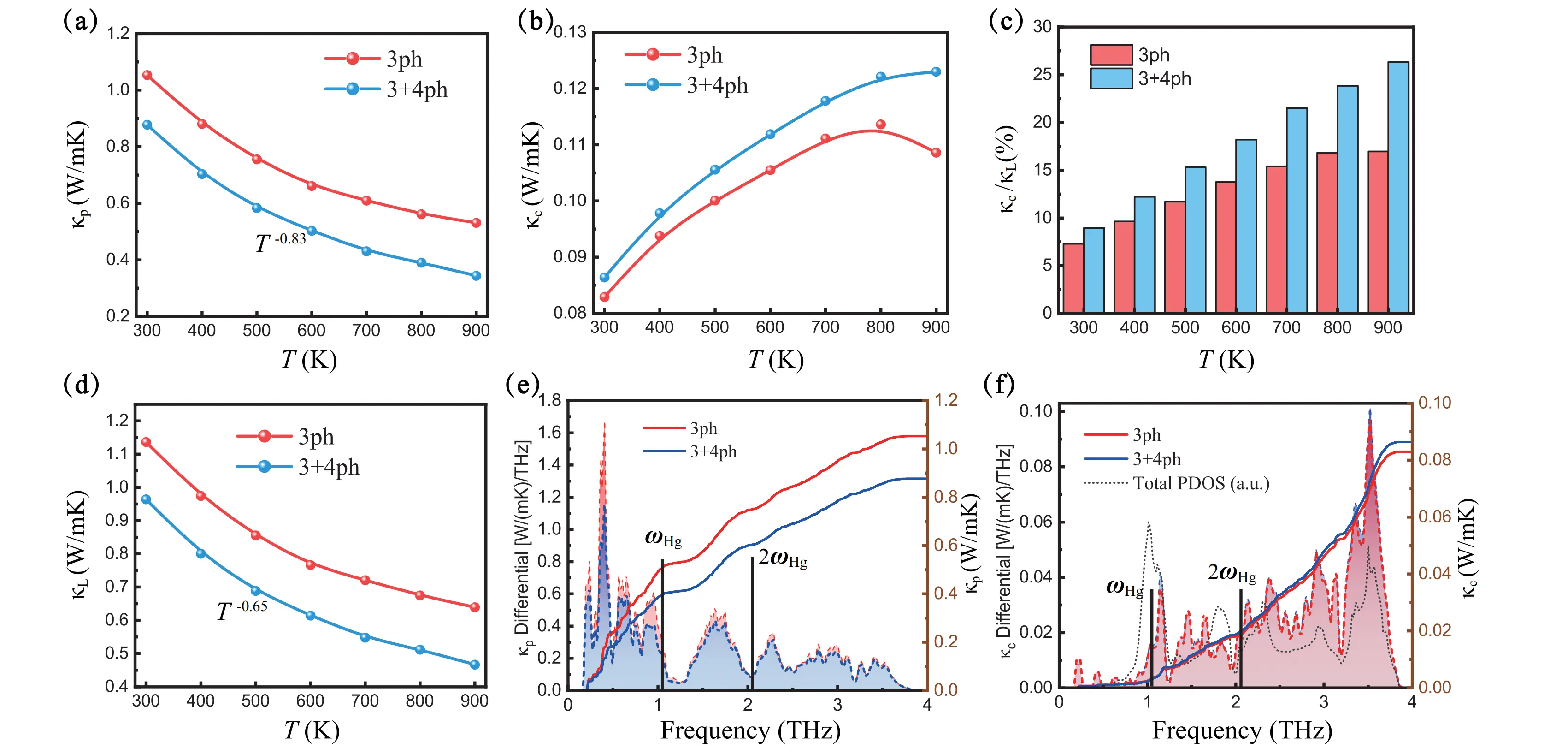
Figure 3. Calculated temperature-dependent (a) κ_p (b) κ_c considering 3ph and 3+4ph scattering; (c) The relative contribution of κ_c to total thermal conductivity κ_L; (d) Temperature-dependent total lattice thermal conductivity κ_L; (e) Cumulative and differential κ_p versus phonon frequency at 300 K; (f) Cumulative and differential κ_c versus phonon frequency at 300 K.

In contrast, Figure 3b demonstrates that κ_c follows an increasing trend with temperature. The 4ph effects enhance this contribution, elevating κ_c from 0.11 W/mK (3ph only) to 0.12 W/mK at 900 K, representing a 9% increase.

The competing temperature dependencies of these components lead to important consequences for the overall thermal transport, as illustrated in Figure 3c. The relative contribution kc/kL grows substantially with temperature, reaching 26% at 900 K when both 3ph and 4ph processes are considered. This enhancement of the glass-like contribution by 4ph scattering highlights the growing importance of wave-like thermal transport at elevated temperatures. Figure 3d presents the temperature evolution of total lattice thermal conductivity κ_L, which exhibits a weaker temperature dependence ${\kappa }_L\propto T^{-0.65}$ compared to k_p ${\kappa }_p\propto T^{-0.83}$ when considering both 3ph and 4ph scattering. This relative stabilization originates from the compensating effects of decreasing κ_p and increasing κ_c with temperature.

The frequency-resolved analysis in Figure 3e reveals that phonons below 1 THz dominate κ_p contributions, accounting for 45% of the total κ_p when including 4ph processes. This predominance stems from their combination of high group velocities and relatively long lifetimes. Two distinct minima appear in the differential κ_p spectrum. Near ω_Hg (1.04 THz), the κ_p suppression results from both the ultralow group velocities of flat rattling modes and enhanced 4ph scattering through redistribution processes (q + q₁ → q₂ + q₃). At 2ω_Hg (2.08 THz), the minimum arises from 3ph emission (q → q₁ + q₂) facilitated by the dense, flat Hg-derived rattling modes that provide abundant final states.

Figure 3f demonstrates a complementary relationship between κ_c and κ_p. The κ_c spectrum shows maximum enhancement at ω_Hg due to 4ph-assisted wave tunneling through the overdamped rattling modes. The peak near 2ω_Hg arises from enhanced wave-like tunneling between the flat phonon branches induced by Hg rattling modes. Both features correlate strongly with the phonon density of states, as the abundant phonon pairs with small ${\omega }_q^s-{\omega }_q^{s^{\prime }}$ differences satisfy the resonance condition for efficient wave-like transport.

To further validate the causal link between rattling modes and phonon scattering, we systematically tuned the Hg-neighbor force constants and examined the resulting changes in phonon dispersion, scattering phase space, and thermal transport. As shown in Figure 4a, doubling the force constants (“Toy” model) significantly hardens the low-frequency flat phonon bands compared to the natural system (“Actual”), indicating suppressed rattling. Correspondingly, the characteristic peaks in the three-phonon emission (Figure 4b) and four-phonon redistribution (Figure 4c) phase spaces nearly vanish, confirming that these scattering channels are intrinsically tied to rattling-induced band flatness.

Display Full Size

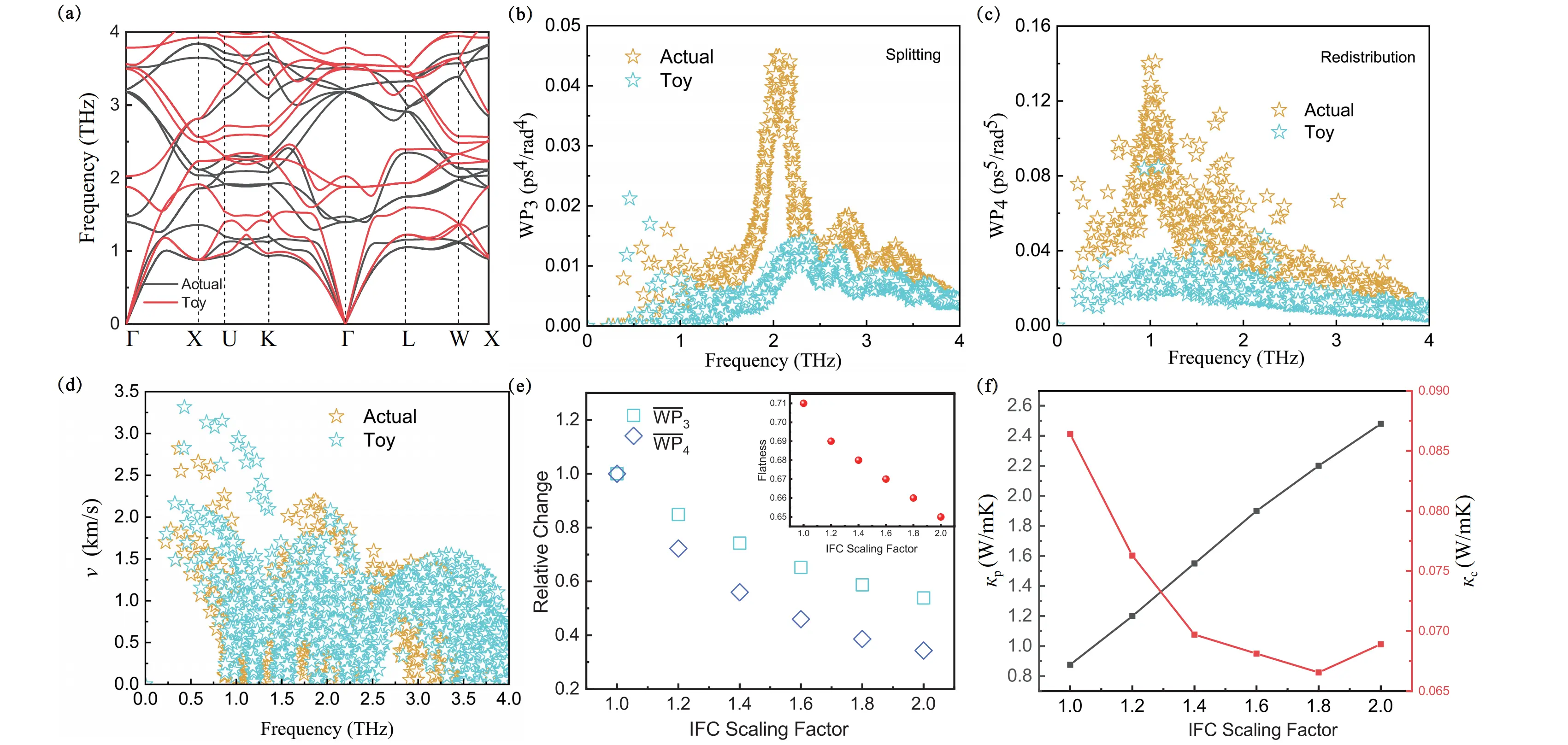
Figure 4. Modulation of Hg-neighbor force constants in Sr₂HgSn. (a) Phonon dispersion: Actual (black) vs. Toy (red); (b) Three-phonon emission phase space comparison; (c) Four-phonon redistribution phase space comparison; (d) Phonon group velocity remains largely unchanged; (e) Evolution of $\overline{W{P}_3}$, and $\overline{W{P}_4}$ with force constant scaling. The inset shows the flatness parameter; (f) Corresponding changes in κ_p and κ_c.

Figure 4d shows that phonon group velocities remain largely unchanged, implying that the thermal conductivity variation stems primarily from scattering modulation rather than velocity suppression. The quantitative decrease in band flatness, together with the reduction in average three-phonon $\left(\overline{W{P}_3}\right)$ and four-phonon $\left(\overline{W{P}_4}\right)$ scattering phase spaces, is summarized in Figure 4e. Here, the band flatness is quantified using the coefficient of variation of acoustic phonon frequencies:

(3)$\text{Flatness}=1-\frac{{\sigma }_{{\omega }_{\mathrm{ac}}}}{⟨{\omega }_{\mathrm{ac}}⟩}$

Where σ_ωac and <ω_ac> denote the standard deviation and mean of acoustic phonon frequencies, respectively. Finally, Figure 4f demonstrates that stiffening the rattling bonds leads to an increase in κ_p and a decrease in κ_c, directly correlating rattling softness with the suppression of lattice thermal conductivity.

Figure 5a,b presents the phonon lifetime distribution as a function of frequency at 300 K and 900 K, respectively, with the scatter point area proportional to each mode’s contribution to κ_L and color-coded by transport mechanism (green for particle-like κ_p, blue for glass-like κ_c). At 300 K (Figure 5a), most phonons lie above the Wigner limit, indicating dominant particle-like thermal transport. The rattling-induced flat phonon branches create a dense population of modes near the Ioffe-Regel limit, suggesting emerging wave-like characteristics.

Display Full Size

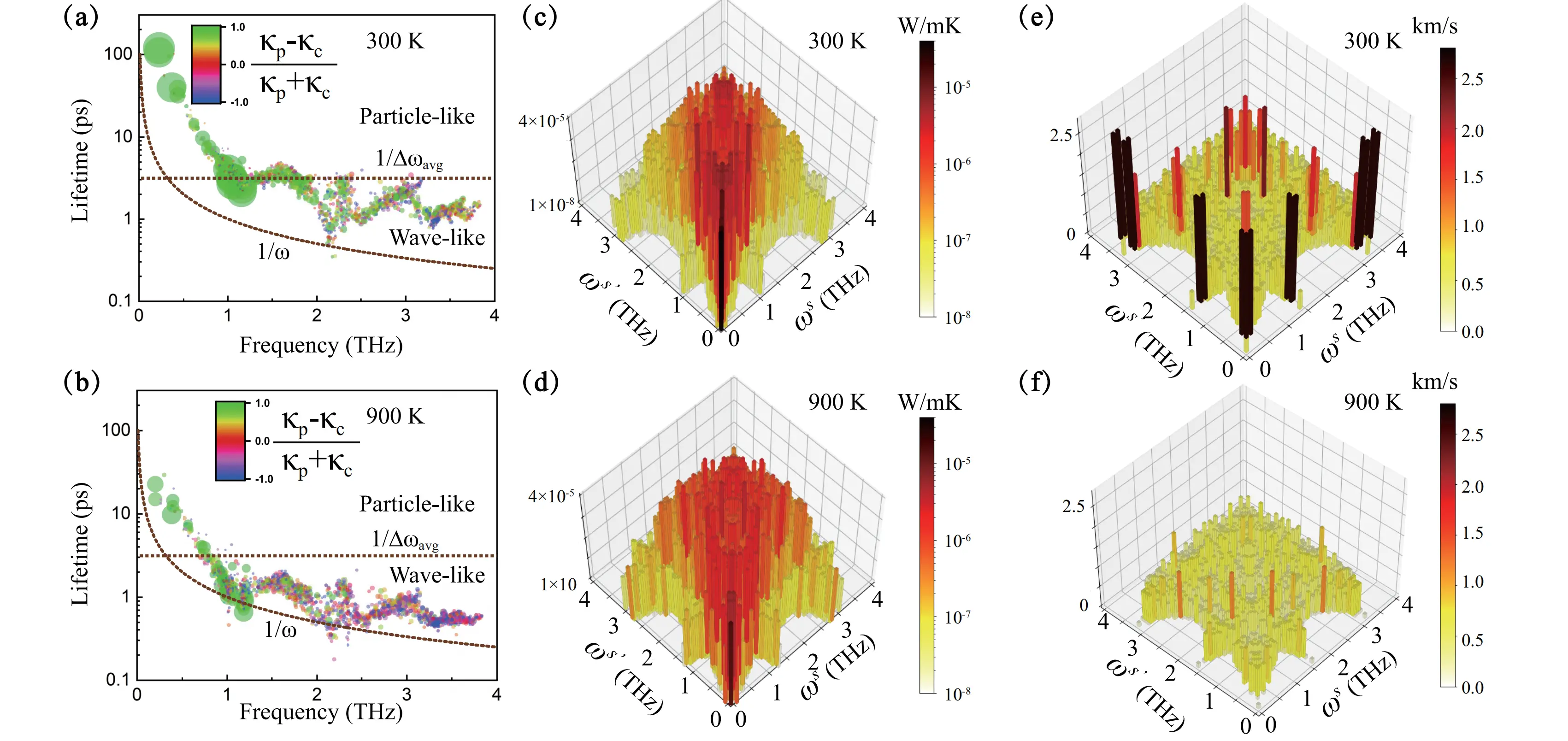
Figure 5. Phonon lifetime versus frequency at (a) 300 K and (b) 900 K, with scatter point areas proportional to their contribution to κ_L (green: particle-like κ_p, blue: glass-like κ_c). The Wigner limit ${\tau }_{\text{Wigner}}=1/\Delta {\omega }_{\text{avg}}$ and Ioffe-Regel limit ${\tau }_{\text{Ioffe-Regel}}=1/\omega$ are shown as orange and red lines, respectively. Resolved κ_c contributions from different phonon pairs at (c) 300 K and (d) 900 K. Interbranch phonon group velocity $v^{s{s}^{\prime }}$ for different phonon pairs at (e) 300 K and (f) 900 K.

With increasing temperature to 900 K (Figure 5b), enhanced phonon-phonon scattering reduces lifetimes, causing a significant portion of modes to shift into the region between Wigner and Ioffe-Regel limits, where wave-like tunneling becomes important. This transition explains the temperature-induced enhancement of κ_c shown in Figure 3.

The origin of wave-like thermal transport is further analyzed in Figure 5c,d, which displays the resolved κ_c contributions from different phonon pairs at 300 K and 900 K. The strong diagonal features confirm that phonon pairs with small frequency differences $({\omega }^s\approx {\omega }^{s^{\prime }})$. In the rattling-mode-dominated 0.9-1.4 THz range, phonon pairs make a considerable contribution to κ_c due to their dense spectral distribution. At 900 K (Figure 5d), the off-diagonal contributions become more pronounced, reflecting the increased importance of phonon pairs with larger frequency differences at elevated temperatures.

To understand the role of interbranch coupling, Figure 5e,f presents the interbranch phonon group velocity $v^{s,s^{\prime }}$ for different phonon pairs. At 300 K (Figure 5e), certain phonon pairs exhibit exceptionally high $v^{s,s^{\prime }}$ values (> 2 km/s). With increasing temperature to 900 K (Figure 5f), the distribution becomes more uniform.

Figure 6 systematically demonstrates how rattling modes at ω₀ influence thermal transport through three distinct mechanisms: (1) The dense phonon spectrum near ω₀ generates large phonon density of states, where small frequency differences $({\omega }^S-{\omega }^{s^{\prime }})$ between neighboring modes significantly enhance the glass-like conductivity (κ_c). (2) The rattling-induced flat bands simultaneously reduce phonon group velocities (suppressing κ_p) while creating favorable conditions for enhanced scattering: the 3ph phase space (WP₃) peaks at 2ω₀ and the 4ph phase space (WP₄) maximizes at ω₀ due to relaxed momentum conservation requirements. These scattering enhancements further reduce κ_p while increasing κ_c. (3) The strong intrinsic anharmonicity near ω₀ additionally boosts 3ph scattering rates, reinforcing the suppression of κ_p and further promoting κ_c contributions.

Display Full Size

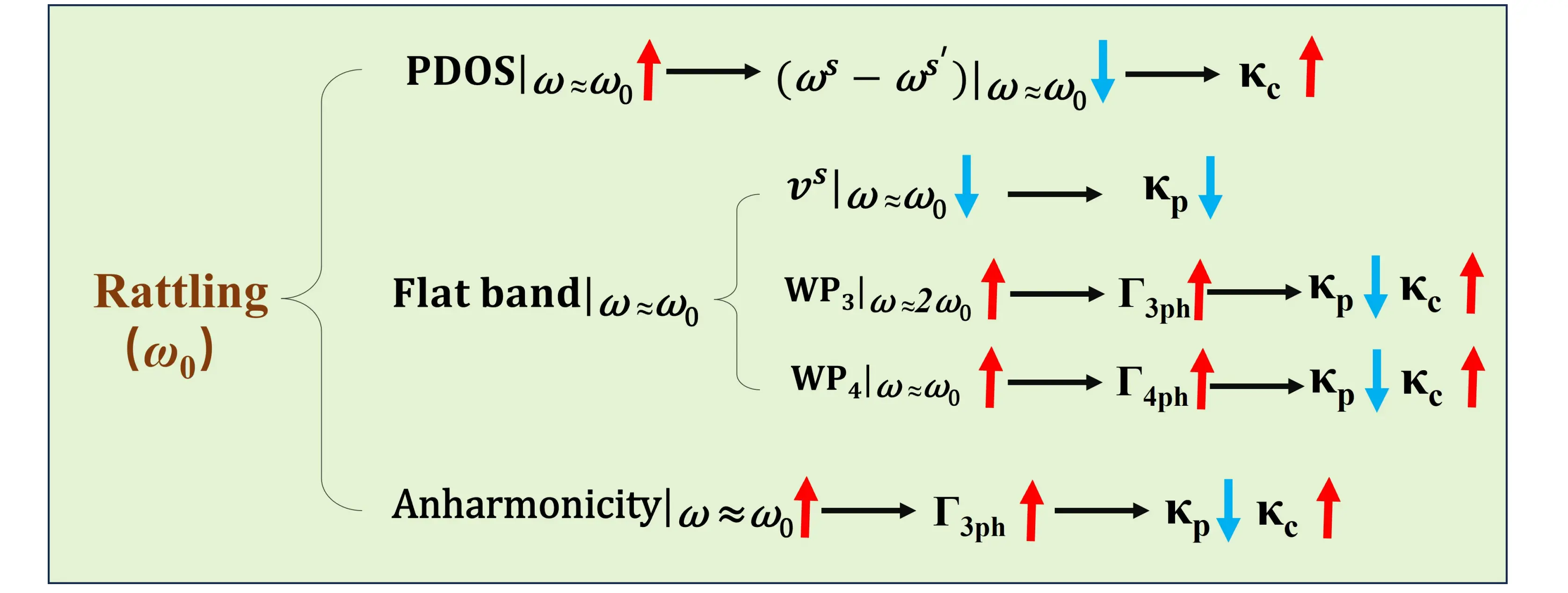
Figure 6. Schematic illustration of rattling mode effects at ω₀ on phonon scattering and thermal transport.

4. Conclusions

This study demonstrates that metallic rattling of weakly bonded Hg atoms in Sr₂HgSn effectively suppresses particle-like thermal conductivity (κ_p) while enhancing wave-like conduction (κ_c). Through force-constant modulation and frequency-resolved analysis, we establish that rattling-induced flat phonon bands simultaneously intensify three- and four-phonon scattering and promote phonon mode hybridization, leading to a frequency-selective crossover between κ_p and κ_c. The resulting competition between suppressed particle-like transport and enhanced wave-like tunneling yields a weak temperature dependence of total lattice thermal conductivity. These findings highlight rattling as a tunable mechanism for dual control of phonon scattering and coherence, offering a design strategy for advanced thermoelectric materials.

Acknowledgements

AI tools were used solely for language editing and polishing of the manuscript. The authors take full responsibility for the integrity, accuracy, and originality of the content.

Authors contribution

Wu Y: Data curation, formal analysis, investigation, methodology, writing-original draft.

Liu Y, Shang L: Investigation, validation.

Zeng S: Formal analysis, software, writing-review & editing.

Liu C: Resources, supervision, writing-review & editing.

Conflicts of interest

There are no conflicts to declare.

Ethical approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and materials

The data and materials could be obtained from the corresponding author upon request.

Funding

This work is supported by Natural Science Foundation of China (Grants Nos. 12304038, 52206092, 12204402), Outstanding Youth Foundation Project of Jiangsu Province (BK20250035), National Key R&D Program of China (Grants No. 2024YFF0508900), and Big Data Computing Center of Southeast University and the Center for Fundamental and Interdisciplinary Sciences of Southeast University.

Copyright

© The Author(s) 2026.