Abstract
Effective scheduling in construction projects increasingly depends on allocating scarce multi-skilled labour under strict precedence and capacity constraints. Reinforcement learning (RL) techniques have presented outstanding performances in addressing Resource Constrained Project Scheduling Problem (RCPSP) instances. However, studies are lacking that utilise RL algorithms in solving extended RCPSP like the Multi-Skilled RCPSP (MSRCPSP). MSRCPSP is a nondeterministic polynomial time (NP)-hard problem that enables activity start times and allocation of multi-skilled resources to be determined simultaneously. Unlike the classical RCPSP, each activity specifies explicit skill requirements rather than anonymous capacity units. This study formulates scheduling as a Markov decision process and compares five optimisation agents, including the genetic algorithm, particle swarm optimisation, black-winged kite algorithm, deep Q-Network (DQN), and proximal policy optimisation (PPO), on benchmark instances from the MSLIB library. The results showed that solutions produced by PPO and DQN concentrate near the reference optima. PPO, in particular, attains the largest number of optimal or near-optimal schedules and the shortest makespans. In several instances, the deep reinforcement learning (DRL) agents also outperform the benchmark solutions, plausibly because CPLEX, constrained by a 60-second time limit, returns suboptimal solutions. Overall, the comparative results provide a practical benchmark of widely used heuristics and metaheuristics against DRL baselines, offering guidance for future algorithm selection and hybridisation for MSRCPSP.
Keywords
1. Introduction
Scheduling is a significant part of project management, since it measures the timeline and resources required for a project. The construction industry faces persistent scheduling challenges under tight resource constraints and specialised skill requirements. Over 70% of construction projects experience delays, and 75% of those run more than 50% over budget due to scheduling delays[1-3]. Therefore, it is crucial for companies to manage projects and scheduling effectively.
Resource-constrained progress scheduling problem (RCPSP), as a critical section of project scheduling that optimises project schedules considering task precedence and resource availability[4-6], has attracted wide discussion since the late 1960s[7]. All tasks require various quantities of resources for completion, where resources are limited[8]. In more realistic situations, the handled skill types and levels can also vary among resources such as workers. Construction projects must coordinate multi-skilled labour teams and equipment under precedence and timing constraints to avoid costly downtime and delays. This motivates the development of advanced scheduling solutions that can handle resource limitations and skill dependencies inherent in real-world construction projects. To achieve this, researchers extend the classic RCPSP to the more realistic Multi-Skill Resource-Constrained Project Scheduling Problem (MSRCPSP). In MSRCPSP, the implementation of activities requires skills and resources that refer to workers and equipment. Each individual possesses a specific set of skills that can be applied to activities that require these[9,10]. MSRCPSP is a nondeterministic polynomial time (NP)-hard problem, and its complexity increases with the number of possible combinations of skill-resource allocation schemes and scheduling decisions[11,12]. The problem was first addressed in the early 2000s, with pioneering research conducted in different fields of project scheduling. For example, considering that scheduling with a limited number of skilled labour is a major challenge in almost all construction projects, Hegazy et al. proposed a multi-skill labour scheduling heuristic algorithm that alleviates resource bottlenecks by allocating idle labour[13]. Besides, the studies performed by Bellenguez-Morineau and Néron in the field of operations research laid the foundations for adopting exact algorithms to solve MSRCPSP by proposing branch-to-bound techniques to handle skill substitution and avoid resource subset enumeration[11,14,15]. Researchers have explored diverse approaches for solving MSRCPSP since, from mathematical optimisation to metaheuristics, where deterministic methods and heuristics attract more attention because of the computational complexity of the multi-skill variant[16].
Notably, there is a lack of research that has utilised deep reinforcement learning (DRL) techniques to solve MSRCPSP. Besides, as claimed by Cai et al., there is a high potential to apply DRL methods to static and dynamic RCPSP with different variant types, such as MSRCPSP[17]. Therefore, in this study, a DRL framework is developed for solving MSRCPSP. Our research approach formulates the project scheduling process as a Markov Decision Process (MDP) in which a learning agent makes scheduling decisions, for instance, selecting the next activity to start and allocating appropriate skilled resources at each time step. The integrated DRL allows the agent to learn from trial and error, thereby understanding the scheduling policy and constructing high-quality schedules. To investigate the efficiency of rreinforcement learning (RL)- and DRL-based techniques in solving MSRCPSP, we selected five representative algorithms to optimise the scheduling policy, including genetic algorithm (GA)[18-20], Particle Swarm Optimisation (PSO)[21-22], Black-Winged Kite Algorithm (BKA)[23-25], Deep Q-Network (DQN)[26], and Proximal Policy Optimisation (PPO)[27-29], and compared the scheduling results from the five approaches. While previous studies[17] also compared the performance of a PPO-based agent against other algorithms in solving scheduling problems, most of them did not consider the additional multi-skill variants in practical project instances, which can increase the complexity of RCPSP. Besides, the five representative optimisation algorithms included in this study have not been compared in other studies in the research domain of scheduling optimisation. The agents are trained and tested using the instances provided in the series of MSLIB benchmark datasets.
The main contributions of this study are listed below:
1. A unified MSRCPSP benchmarking framework is proposed, which integrates GA, PSO, BKA, DQN, and PPO within a common decoder, objective, and constraint handling.
2. The solution comparison of the five integrated agents is performed. Experiments show that PPO outperforms the other four algorithms in solving MSRCPSP and has the capability to provide satisfactory scheduling solutions and good generalisation performance.
The remaining sections of this article are organised as follows. Section 1.1 presents an introductory background of this study. Section 2 provides a description of the concept and logic of the applied algorithms, as well as the MDP model formulation. The next section exhibits and compares the solution outcomes from the five integrated agents. Section 4 discusses the outcome comparison and the limitations of the approaches, as well as the potential research directions for future studies. The last section concludes the study and reveals the implications of the research for academia and industry.
1.1 Introductory background
A rich body of research has been conducted to solve RCPSP and its multi-skill variants using different methods, primarily consisting of exact optimisation algorithms and heuristic optimisation algorithms[1]. Although exact optimisation algorithms like Integer Programming[30] and Branch-and-Price methods[31] can find optimal schedules for small instances, they are often considered inefficient and time-consuming[1]. On the other hand, due to their high efficiency, researchers prioritise the use of heuristic algorithms to solve RCPSP-related issues[32-35]. Heuristic methods often extend the classic priority-rule or greedy algorithms from RCPSP to account for multi-skill considerations. For instance, Myszkowski et al.[36] proposed a novel scheduling heuristic method for MSRCPSP and compared the method’s performance with the state-of-the-art priority rules. Experiments were conducted using a created dataset of instances and proved that the proposed method can be applied to more complex scenarios[36]. Brooks[37] developed a parallel scheduling heuristic method based on the Parallel Scheduling Scheme (PSS)[37], and integrated resource weight and activity grouping concepts to solve MSRCPSP considering the multi-skill nature of the involved resources. The study demonstrates the feasibility of adapting activity priority rules to address MSRCPSP[38]. More comprehensively, Yu et al.[39] targeted the stochastic distributed multi-project RCPSP with multi-skill staff and introduced a two-stage model with 12 priority rules. Compared with other existing approaches, the two-stage model with two out of 12 priority rules outperforms other approaches, particularly in more complicated instances. Moreover, experiments also suggest that the proposed method can achieve shorter CPU runtimes on distributed problems compared to centralised methods[39]. However, the approach is only applicable to large instances, which limits its application to specific scenarios. In addition, Akbar et al.[40] targeted the potential underutilisation of labour resources caused by varied task durations and developed an innovative greedy and parallel scheduling algorithm, which aims to allocate surplus resources efficiently to project tasks and reduce resource waste, resulting in a decrease in the makespan. The proposed algorithm was compared with the PSS approach by Almeida et al.[38], and outperformed the PSS method in minimising project duration. These heuristic methods address the challenge of fast decision-making in dynamic or large-scale projects by providing a feasible schedule quickly, which can be useful as an initial solution or for real-time adjustments. However, pure heuristics may sometimes yield suboptimal results. Thus, they are often hybridised with more powerful metaheuristic searches in recent studies.
Metaheuristics have dominated MSRCPSP research since 2010, given their success in exploring large solution spaces under complex constraints. A wide range of metaheuristic algorithms has been applied, including genetic algorithms, swarm intelligence methods, and hybrid/meta-hybrid techniques. GA, which is an optimisation method inspired by Darwinian theory of evolution[18,19], is one of the most popular choices for MSRCPSP. It operates through iterative cycles of selection, crossover, and mutation, evolving a population of candidate solutions toward better fitness values. Campos et al.[41] developed a GA for an open-shop scheduling variant with multi-skill resource constraints. The approach achieved competitive results by combining GA’s global search with local improvement and was compared with an Ant Colony Optimization (ACO) method. The study highlighted the effectiveness of both evolutionary search and pheromone-based constructive search. ACO tackles the MSRCPSP by modelling the scheduling problem as a path construction task for ants. The study by Campos et al.[41] also showed that ACO can construct high-quality multi-skill schedules by iteratively improving task sequences based on pheromone trails, in parallel with their GA approach. PSO is also one of the swarm and nature-inspired algorithms that has been commonly adapted for RCPSP. It guides resource assignment and scheduling decisions by treating each potential schedule as a “particle” moving through solution space. PSO, which was developed by Kennedy and Eberhart, is a robust stochastic optimisation method used to analyse the structure or necessary parameters and optimise a critical target[21,42]. The concept of the algorithm is rooted in swarm intelligence[43], where a group of simple agents collectively exhibits intelligent global behaviour by following simple local rules. For example, Zhang et al.[44] proposed a solution-solving scheme for RCPSP based on the PSO principle to minimise the project duration. The proposed PSO-based method was compared with other algorithms like GA and simulated annealing and presented outstanding performance in solving RCPSP. More recently, Jia and Guo[45] integrated the artificial bee colony (ABC) and PSO algorithms to improve the efficiency of RCPSP solutions. Experiments showed that the proposed ABC-PSO approach demonstrated clear advancement over traditional ABC, PSO, and a few other heuristic algorithms. However, only a few studies have adopted PSO for solving MSRCPSP, which leaves room for further research.
Various RL approaches have also been integrated to solve scheduling problems and have achieved competitive performances compared to traditional methods[46,47]. While traditional algorithms require manual adjustment for different problems, RL can achieve self-learning about scheduling strategies[17]. Early RL applications to RCPSP focused on classical RL methods, such as tabular Q-learning or policy iteration, sometimes combined with traditional methods like heuristic frameworks and variable neighbourhood search[17]. The RL technique was first integrated by Choi et al.[48] to solve stochastic RCPSP with dynamic project arrivals. The developed Q-Learning-based approach allows researchers to derive empirical state transition rules from the data, and a MDP model was developed to formulate the scheduling policy[48]. Yet, the method was not validated on other RCPSP types, which can limit its generalisability[17]. Jędrzejowicz and Ratajczak-Ropel introduced an RL-based strategy to assist an A-Team of asynchronous optimization agents for solving RCPSP. Four heuristic algorithms were incorporated into the approach, and an RL agent dynamically determined which heuristic agent to invoke next, based on the current state of the search. This work confirms the capability of a classical RL controller in improving a meta-heuristic search process for RCPSP by adaptively selecting the most promising heuristic at each step[49]. Sallam et al.[50] proposed an RL-based meta-heuristic switching method that merges multiple algorithms in a single algorithmic framework. The RL technique is utilised for algorithm selection based on population diversity and solution quality to address uncertainty. However, the approach did not consider the impacts of dynamic resource availability and demand. Besides, the research assumed that the tasks are non-preemptive, which means that a task can only be started after the previous task has finished. Such a task feature may not be practical in real-life projects[50]. Another innovative approach was introduced by Szwarcfiter et al.[51]. To overcome the challenges potentially caused by uncertain activity durations, the researchers employed RL to achieve three project management goals that include 1) to maximise project performance while considering both schedule and budget constraints, 2) to minimise the project schedule duration with the requirements of resource constraints and task durations, and 3) to balance the project value and its net present value (NPV) while considering the aforementioned restrictions[51]. Zhang et al.[52] also noticed the existing challenges in maximising projects’ NPV due to the inherent uncertainties associated with large-scale projects. The study proposed a three-level reinforcement learning framework that comprises the resource assignment level, work package level, and project level. Among the three levels, a Q-Network-based method was utilised at both the work package level and project level to maximise the expected NPV for each work package as well as the entire project[52].
Another important technique for solving scheduling problems is DRL. Deep learning has been widely applied in RL across various fields, such as games, robotics, and natural language processing. The representation learning within deep learning allows for automatic feature engineering and end-to-end learning through gradient descent, and is adaptive to different scheduling conditions that contain various tasks and resource information, which heavily reduces the dependency on domain knowledge and human intervention[53,54]. An increasing number of studies have been conducted to develop DRL-based RCPSP solutions. For instance, Zhao et al.[54] integrated the classical PPO and graph neural network (GNN) to develop an end-to-end DRL approach to obtain competitive priority rules for RCPSP. Similarly, Cai et al.[17] developed a framework consisting of RL algorithm, specifically PPO, and GNN to solve RCPSP and further RCPSP with uncertain resource allocation. The GNN-based structure was developed to extract information from problem data and map it to perform a probability distribution through the policy network, while the PPO was employed for end-to-end model training. Although the approach performed well on most instances, the target problem type is limited to traditional RCPSP and RCPSP with resource disruption. In addition, an RCPSP with ladder-type carbon trading prices was proposed by Liu et al.[55] to minimise total carbon emissions. A multi-step double deep Q-Network was trained to learn the scheduling policy, and a tabu search algorithm was employed to further enhance the solution. The outcomes of the proposed method were compared with the results achieved by other algorithms like normal tabu search and genetic algorithm, which showed the outperformance of the proposed approach. Yet, the static deterministic condition of the focused problem limits the proposed approach from being adopted in practical projects.
2. Methodology
2.1 Description of target problem and overall methodology
The traditional RCPSP is normally described as follows[17,56,57]: Imagine that a project is described by an activity-on-node (AON) network G = (V, E), where V = {0, 1, ..., n + 1} is the set of vertices that represent the activities and E denotes the set of edges describing the precedence relationships among the activities. The activities are numbered from 0 to n + 1, since the starting and ending activities of a project are considered to be dummy activities. The duration of each activity is represented by di (0 ≤ i ≤ n + 1), and the starting and ending time of activities are denoted by starti (0 ≤ i ≤ n + 1) and endi (0 ≤ i ≤ n + 1) respectively. Ri stands for the resource capacity requirement for performing activity i (0 ≤ i ≤ n + 1), and there are K renewable resource types required for executing the project. Each activity i requires a certain number of renewable resources rik from each resource type k ∈ R, and therefore Ri = (ri1, ri2, ..., rik). It is assumed that all resources are renewable, meaning that the resources occupied during a preceding activity become reusable once that activity is completed.
The MSRCPSP extends the traditional RCPSP by incorporating skill requirements into the scheduling problem. This scenario is particularly relevant to construction projects, where tasks often require specific skills from resources (workers, machinery operators, etc.). Here, each activity has specified skill demands, and each resource possesses certain skills. The goal remains to minimise the total project duration, with added complexity arising from matching skill demands with resource capabilities. Formally, MSRCPSP involves scheduling activities subject to precedence constraints, resource availability, and skill matching requirements, aiming to minimise the makespan. Each activity requires certain skill levels qis for each skill si ∈ S, and each resource possesses specific skill levels Qrs for each skill si ∈ R.
In summary, there are several assumptions for the MSRCPSP in this study. Firstly, each activity is executed in only one mode. Since our primary focus is joint sequencing and multi-skill allocation, performing solutions under a consistent project mode can effectively control experimental variables. Secondly, as commonly required in MSRCPSP, each activity requires certain skill types and certain levels of skills to finish. Thirdly, an activity can start immediately after the completion of the preceding activity. Besides, each of the skilled resources can only be assigned to one activity at a time. Such an assumption mirrors on-site practice and avoids fractional allocations that are rarely feasible for human crews. Lastly, once an activity is started, it cannot be interrupted. For most construction tasks, interruption incurs significant setup, safety, and efficiency costs. Modelling activities as non-preemptive matches real-life practices. Five algorithms were utilised to solve the MSRCPSP individually, and their performances were compared afterwards.
2.2 The integrated algorithms
The scheduling agent integrates five distinct algorithms: GA, PSO, BKA, DQN, and PPO. GA, PSO, and BKA serve as heuristic and metaheuristic methods to explore and optimise scheduling solutions iteratively, whereas DRL approaches, including DQN and PPO, model the scheduling problem as an MDP. Since GA and PSO are commonly applied in RCPSP/MSRCPSP studies as classical baselines, adopting these agents can anchor the performance of DRL-based approaches to widely recognised methods. BKA reflects recent nature-inspired advances with stronger diversification via heavy-tailed moves. In the DRL framework, the agent dynamically learns optimal scheduling policies through interactions with the environment. DQN provides the canonical action-value learning baseline for discrete decisions, while PPO represents the current standard for stable policy-gradient optimisation. These methods offer complementary exploration–exploitation behaviours and learning biases, and can be implemented with a shared decoder, objective, and time budget. In this section, we describe the process of adopting the five algorithms to develop the agents.
2.2.1 Genetic algorithm
The GA used in this study follows the standard evolutionary principles of selection, crossover, and mutation, yet it has been adapted to address the discrete and skill-dependent characteristics of the MSRCPSP. Instead of using a generic continuous search space, each chromosome in this implementation encodes a feasible activity sequence and its corresponding skill assignments. Candidate solutions are represented as real-valued vectors, with the initial population generated randomly and evaluated using a user-defined fitness function. The objective function f(x) evaluates the makespan of the decoded schedule, incorporating penalty terms for any constraint violations. The selection phase adopts roulette-wheel selection (Baker, 1987), where the probability pi of selecting individual i is defined as Equation (1), ensuring that solutions with smaller makespan have a higher selection probability. Selected parents undergo simulated binary crossover[58], which generates two offspring from parents x(1) and x(2) using Equation (2) and Equation (3).
where the spread factor β is drawn from a distribution controlled by the crossover index ηc. This mechanism enables both interpolation and limited extrapolation between parental solutions. Polynomial mutation is then applied to each decision variable xk with a mutation probability pm, which introduces small local perturbations or larger directional jumps with lower probability:
Here, δk is determined by the mutation index ηm. Mutation ensures diversity in the population and mitigates premature convergence. After variation operators are applied, all offspring are evaluated using the decoding function, and an elitist truncation strategy retains the best N individuals to form the next generation. The best solution (x*, f(x*)) is updated when a new individual achieves a smaller makespan than the current best. This process repeats for a predefined number of generations. Lastly, the best solution undergoes a repair phase to ensure full feasibility in resource and skill assignments before generating the final schedule. The algorithm uses fixed crossover cp = 0.7 and mutation probabilities mp = 0.1, though the code hints at adaptive strategies. While elitism and local search are not explicitly used, the implementation is aligned with common GA practices and is well-suited for solving complex continuous optimisation problems.
2.2.2 Particle swarm optimisation
We also apply and tailor PSO as a standalone optimiser to solve the MSRCPSP by efficiently exploring the solution space of task-resource-skill assignments and scheduling sequences. A swarm of N particles encodes candidate schedules in a continuous decision vector xi ∈ RD documenting the particle locations, where each particle represents a possible schedule, expressed as a list of numbers. Each particle has a velocity vi that guides its motion through the search space, adjusting its position based on both its own past success and the success of the best-performing particle in the group. At iteration t, velocities are updated by the standard PSO rule
Where ω = 0.8 is the inertia weight, c1 = c2 = 1.1425 are the cognitive accelerations, r1, r2~U(0, 1)D inject stochasticity, pi is the best-known solution for particle i, and g is the global best. The use of both global and personal bests enables a balance between intensifying search in promising regions, namely exploitation, and scanning unexplored areas, which is called exploration. Infeasible transitions that would violate skill compatibility or activity order are corrected using a boundary-checking mechanism, while random perturbations are applied to preserve population diversity. To prevent unstable steps, velocities are controlled with the range [vmin, vmax] = [-0.5, 0.5]. Positions are then advanced as
with a random factor η~U(0, 1)D that diversifies steps. To further maintain population diversity and mitigate premature convergence, a mutation-like perturbation resets each dimension of xi to a fresh U(0, 1) draw with probability of 0.1. The objective function f(x) evaluates makespan and constraint penalties, which are minimised to guide the search. Individual and global records are updated greedily: if f(xit+1) < f(pi), then pi = xit+1; if f(xit+1) < f(g), then g = xit+1. The algorithm records the best fitness value per iteration in the history array, enabling performance tracking and convergence analysis.
2.2.3 Black-winged kite algorithm
The BKA is a nature-inspired swarm intelligence optimiser proposed in 2024, modelling the hunting and migratory behaviour of the black-winged kite bird[23,59]. It is a meta-heuristic algorithm designed for continuous optimisation problems, where a population of candidate solutions iteratively searches for the optimal solution. Algorithmic mechanisms like Cauchy-based mutation and leader-guided search are offered in the BKA, which are specifically designed to balance global exploration and local exploitation. As Wang et al.[23] claimed, BKA integrates the Cauchy mutation strategy with the leader strategy to enhance global search capabilities and accelerate convergence. Compared to classical methods, this algorithm demonstrates superior performance on benchmark functions and engineering optimisation tasks. Thus, by including BKA, we gain insight into how a modern, mutation-driven leader-based swarm method behaves in MSRCPSP, and whether its balance of exploration and exploitation offers advantages over GA, PSO, or pure RL-based agents in a highly constrained scheduling domain.
In each searching iteration, the algorithm performs two major phases inspired by the black-winged kite’s behaviour: an attacking phase and a migration phase. The population can be initially seeded with random candidate solutions. Some implementations enhance this initialisation using chaotic maps to distribute initial solutions more uniformly and improve diversity[60]. The mathematical model for the attacking phase is shown in Equation (7) and Equation (8) below:
Here,
Following the attack updates, BKA simulates the migration behaviour of black-winged kites, where the flock is guided by a leader bird during long-distance travel. In the algorithm, the leader is the current best solution. The migration update allows each individual to adjust its position relative to the leader’s position while incorporating random fluctuations to avoid premature convergence. Mathematically, the migration phase update for an individual is often described as follows:
where
2.2.4 Deep Q-network
The DQN agent is adapted in this study as one of the schedule optimisation approaches. The DQN agent was initially developed by Mnih et al.[26] and is capable of combining reinforcement learning and artificial neural networks, known as deep neural networks, which can directly study successful policies from high-dimensional input using end-to-end RL. This approach treats scheduling as a sequential decision-making process: at each step, the agent must choose the next task to start, given the current state of the project. In the classic Q-learning method, the quality of a given action a in a state s is quantified by a Q-value, which represents the expected cumulative reward from s if action a is taken and the optimal policy is followed. The goal of Q-learning is to approximate the optimal action-value function Q*(s, a) that satisfies the Bellman optimality equation, which is formulated as
where r is the reward for taking action a in state s, s’ is the next state, and γ (typically 0 < γ < 1) is a discount factor that impacts future rewards[26]. To avoid failure in converging Q(s, a) to Q*(s, a), DQN employs a neural network Q*(s, a; θ) with the parameter θ to approximate the Q-function[61]. Instead of a table of state-action values, the network takes a state as input and outputs Q-values for all possible actions. The network parameters are trained to minimise the error between its Q-value predictions and the target values computed from the Bellman equation. Specifically, DQN uses a loss function based on mean squared error:
Here, y = r + γmaxa’Q(s’, a’; θ) is the target Q-value, and θ denotes the parameters of a target network. The DQM network in our code is a fully-connected feedforward neural net with a hidden layer of 256 ReLU neurons that outputs an estimated Q(s, a) for each potential action a. A key enhancement here is action masking, where infeasible actions are excluded from the agent’s choices so that their Q-values do not influence the decision, improving both learning efficiency and the quality of the resulting schedules. The agent receives negative rewards proportional to task delays and is rewarded upon successful project completion, thus learning to minimise total project duration. This aligns with traditional objectives in construction project scheduling while allowing the model to autonomously learn optimal or near-optimal task sequences.
2.2.5 Proximal policy optimisation
PPO is an on-policy, actor-critic method in RL that simplifies earlier trust-region approaches by using a clipped surrogate objective, which is widely recognised for its balance between implementation simplicity and performance[27]. The actor represents the GNN and policy network, while the critic uses the same GNN layer as the actor. The algorithm also shows greater stability than other RL algorithms[17]. A neural network outputs the probability distribution of possible actions for the agent, and the value function V(s) predicts expected returns from a given state. The action probability is computed using a softmax over the logits, providing a stochastic policy
As discussed by previous studies, applying the original policy gradient to update parameters often results in unexpectedly large-scale policy updates, which can cause parameters to deviate from their original positions and thus negatively impact the previous results. The core PPO update in this study employs a clipped surrogate objective rather than a KL divergence constraint to prevent excessively large policy updates. Mathematically, this is expressed as
where
Here, δ = rt + γVθ(St+1) - Vθ(St) and Vθ(St) refers to the value function to estimate state value[17]. Moreover, an entropy term is included to encourage exploration by maximising the randomness in action selection, ensuring the agent does not converge prematurely to suboptimal solutions. Through repeated trajectory collection, the model can iteratively improve its scheduling policy to minimise target project duration.
2.3 MDP formulation
In both the DQN- and PPO-based implementations, the scheduling problem is cast as a MDP in which an agent sequentially selects activities to schedule to minimise the project’s makespan. At each decision epoch t, the state st is represented by a binary vector indicating which activities have already been scheduled; the action at corresponds to choosing the next unscheduled activity. By executing at, the developed model computes the earliest feasible starting and finishing times, as well as the resulting increase in project duration Δt, considering the precedence relations and multi-skill resource availability. The agent then receives the reward rt = -Δt, which penalises schedule prolongation, and observes the next state st+1. Illegal actions, such as selecting an already scheduled activity, immediately terminate the episode with a large negative penalty, whereas completing all activities yields a positive terminal bonus. In the DQN agent, a deep Q-network approximates the action-value function Q(s, a) and is trained off-policy via experience replay and target networks. In the PPO agent, an on-policy actor-critic framework is employed. The actor network parameterises a stochastic policy over available actions, and the critic network estimates the state-value VΦ(s), which are both updated by maximising a clipped surrogate objective using advantage estimates. By formalising scheduling as an MDP with clearly defined states, actions, rewards, and transitions, these DRL agents learn dynamic scheduling policies that adaptively trade off short-term gains against long-term makespan minimisation.
3. Result
Computational experiments have been performed to evaluate the performance of different algorithms integrated in the Methodology section. The model proposed in this study is trained and tested using the MSLIB dataset developed by Snauwaert and Vanhoucke, which is a combined multi-skill project scheduling problem library[9]. The data in the library contain five subsets with different instance sizes and settings of skills and resources, which were converted from four existing datasets with their own research objectives[30,31,38,63]. The optimised project duration is also provided within each instance, which is solved by applying CPLEX with a time limit of 60 seconds or a naïve method if no solution was found within the time limit. In this study, the dataset MSLIB5 was not utilised since it contains empirical project instances whose network, resource, and skill structures are not well-defined[9]. Therefore, 39 instances were selected from MSLIB1-4 to form the training set, leading to a total of 156 instances. Activities in each instance only require one skill type. All coding documents were developed in Python and executed on a Windows 64-bit system with a 3.60 GHz i7-7700 CPU, 16 GB main memory, and an Nvidia GeForce RTX 1080 GPU with 8 GB of RAM.
The MSRCPSP solutions obtained from the five algorithms are presented in Figure 1, where the “X” axes represent different project instances and “Y” axes stand for the calculated project durations. In each graph, the solid triangles denote the theoretical shortest project deadlines, serving as performance baselines, while the hollow circles represent the scheduling solutions obtained by each algorithm. The visual inspection shows that PPO (Figure 1e) and DQN (Figure 1d) consistently produce solutions that are closer to the optimal reference across a wide range of instances, indicating stronger convergence and generalisation abilities. In contrast, PSO exhibits more volatility and often deviates above the baseline, which suggests sensitivity to instance-specific characteristics and potential difficulties in avoiding local optima. GA and BKA, while exhibiting smoother transitions than PSO, also demonstrate moderate variance in solution quality, with performance occasionally matching but frequently falling short of PPO and DQN.
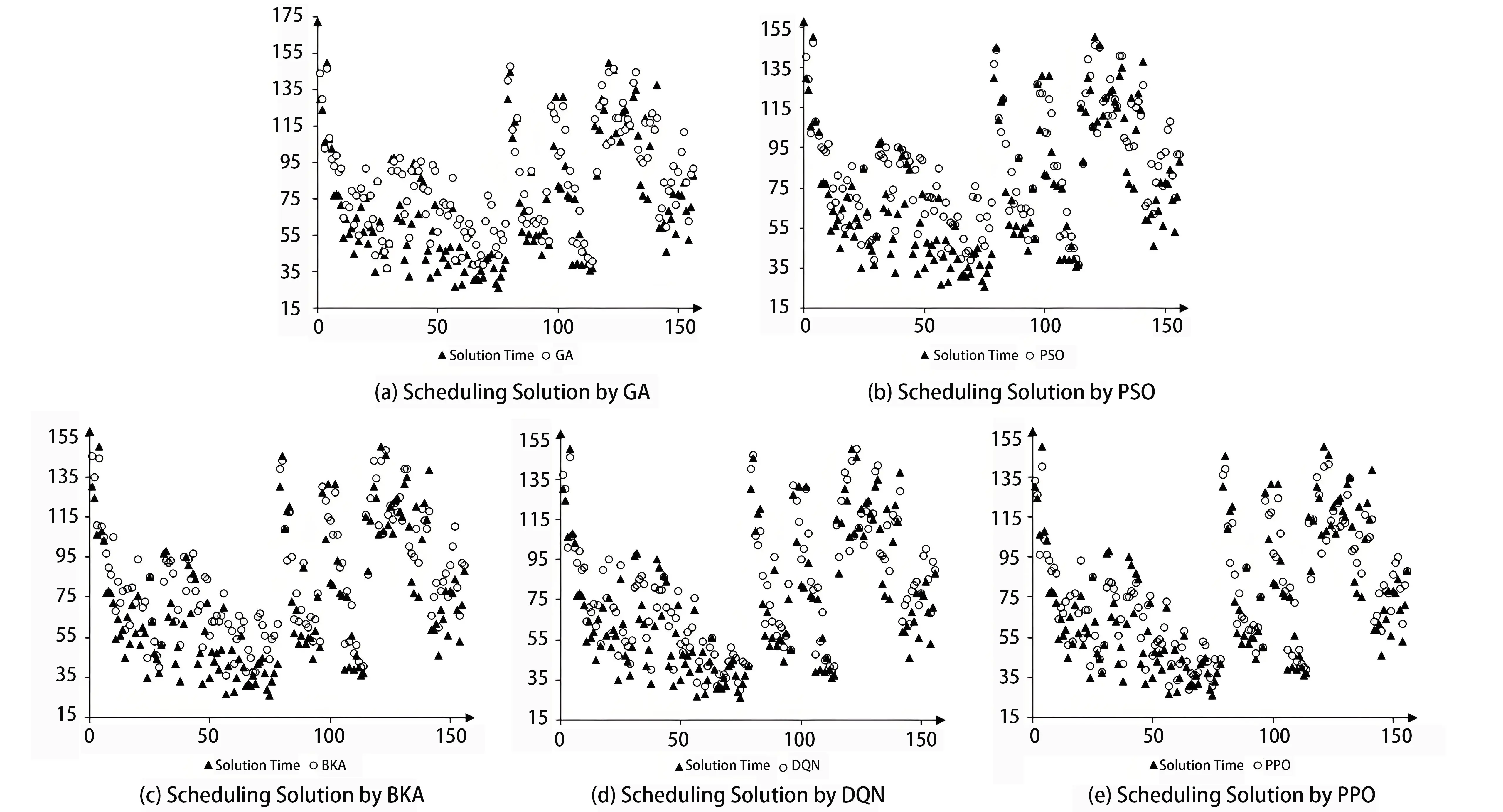
Figure 1. Visualisation of MSRCPSP solution relative error compared to near-optimal schedule. MSRCPSP: multi-skilled resource constrained project scheduling problem; GA: genetic algorithm; PSO: particle swarm optimisation; BKA: black-winged kite algorithm; DQN: deep Q-network; PPO: proximal policy optimisation.
Additionally, Figure 2 shows a comparative analysis of the five algorithms based on the number of project instances for which each agent was able to generate a scheduling solution that falls within a pre-defined satisfactory deadline range. The specific values are also provided in Table 1. As mentioned in the instructions for the MSLIB library[64], the calculated scheduling solution is considered satisfactory if the value falls within the interval from 1 to 1.2 times the given solution by CPLEX. Each sector of the pie chart corresponds to the total count of such successful instances for an employed algorithm, serving as an indicator of overall robustness and reliability across diverse problem scenarios. The pie chart (c) also echoes the scatter diagram in Figure 1. As illustrated, PPO achieves the highest count with 90 satisfactory solutions, indicating superior adaptability and generalisation of learning across the scheduling instances. DQN follows closely behind with a count of 82, further demonstrating the power of deep reinforcement learning methods in managing complex, skill-dependent constraints in MSRCPSP. Both GA and BKA achieved comparable results, each realising 65 successful schedules, suggesting a moderate degree of consistency. Lastly, PSO records the lowest count with 62. Figure 2b,c,d represent the proportions of instances where each algorithm reached optimal or near-optimal deadlines, which highlights the frequency and reliability of each algorithm. Figure 2c shows the proportions of satisfactory solutions generated by each algorithm that lie within the satisfactory solution range. Both Table 1 and Figure 2a present the number of solutions that provide shorter schedules than the optimal deadlines. Although the solutions provided by the data library were solved by CPLEX, which is a powerful optimisation solver, the time limit of 60 seconds may restrict CPLEX’s capability of finding the optimised solution. Therefore, the possibility of generating better scheduling solutions exists. Among the five agents in our study, not only does PPO generate the highest number of satisfactory solutions, it also provides more optimal schedules for 37 project instances. In total, PPO has provided satisfactory schedules or better schedule optimisation in 127 out of 156 instances, further proving the robustness and generalisability of reinforcement learning algorithms in solving MSRCPSP.
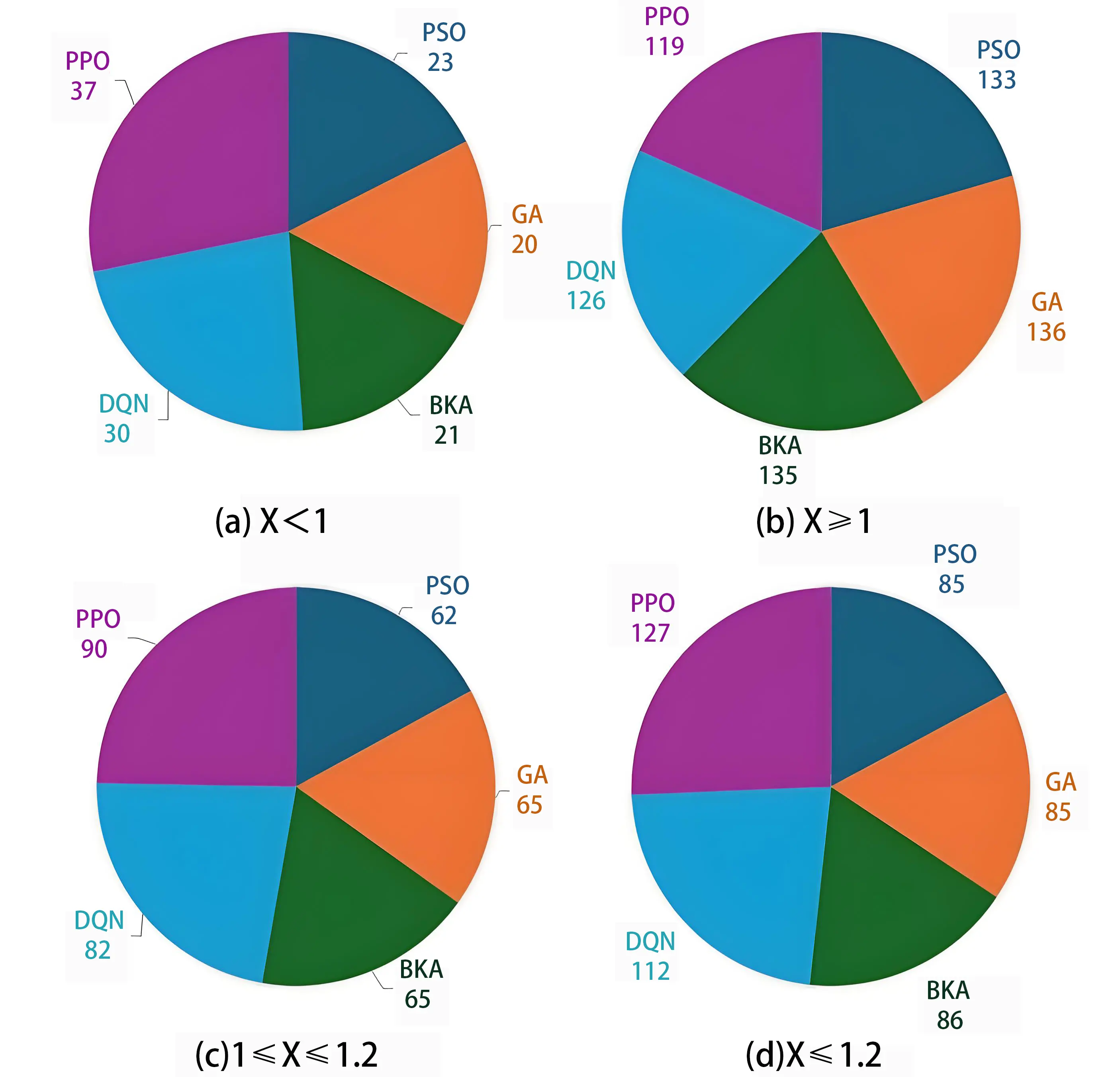
Figure 2. Comparison of satisfactory solution numbers by different agents. GA: genetic algorithm; PSO: particle swarm optimisation; BKA: black-winged kite algorithm; DQN: deep Q-network; PPO: proximal policy optimisation.
| 1 ≤ X | 1 ≤ X ≤ 1.2 | X ≥ 1 | X ≤ 1.2 | |
| PSO | 23 | 62 | 133 | 85 |
| GA | 20 | 65 | 136 | 85 |
| BKA | 21 | 65 | 135 | 86 |
| DQN | 30 | 82 | 126 | 112 |
| PPO | 37 | 90 | 119 | 127 |
PSO: particle swarm optimisation; GA: genetic algorithm; BKA: black-winged kite algorithm; DQN: deep Q-network; PPO: proximal policy optimisation.
4. Discussion
As aforementioned, we observed that DRL-based approaches, including DQN and PPO, yielded higher project values and shorter schedules on MSRCPSP instances compared to heuristic and metaheuristic algorithms, with the PPO-based scheduling agent consistently demonstrating superior performance. To visualise the scheduling solutions, the detailed solution processes of the selected instances are also generated. Since PPO provides the highest count of optimal solutions and the shortest schedule in most cases, a PPO-solved schedule is presented as the visualisation example. Figure 3 presents an example AON diagram based on the selected project instance. The diagram clearly demonstrates the workflow and preceding relationships among the tasks. Figure 4 shows the visualisation of the same solution example, where the x-axis represents the accumulated time of the project and the y-axis denotes the resource usage of each activity. Each rectangular block corresponds to a task labelled with its ID, whose width reflects its duration and height indicates the level of resource consumption. The schedule demonstrates how multiple tasks are arranged sequentially and concurrently while respecting the maximum resource capacity of four units. In the provided example, multiple tasks in the early phase overlap with each other, whereas around day 80-90, tasks like 11, 24 and 14 are conducted in order, fully utilising the available resource capacity. There are only 4 skilled resources available throughout the project lifecycle, which has not been exceeded by the resource usage in the generated solution.
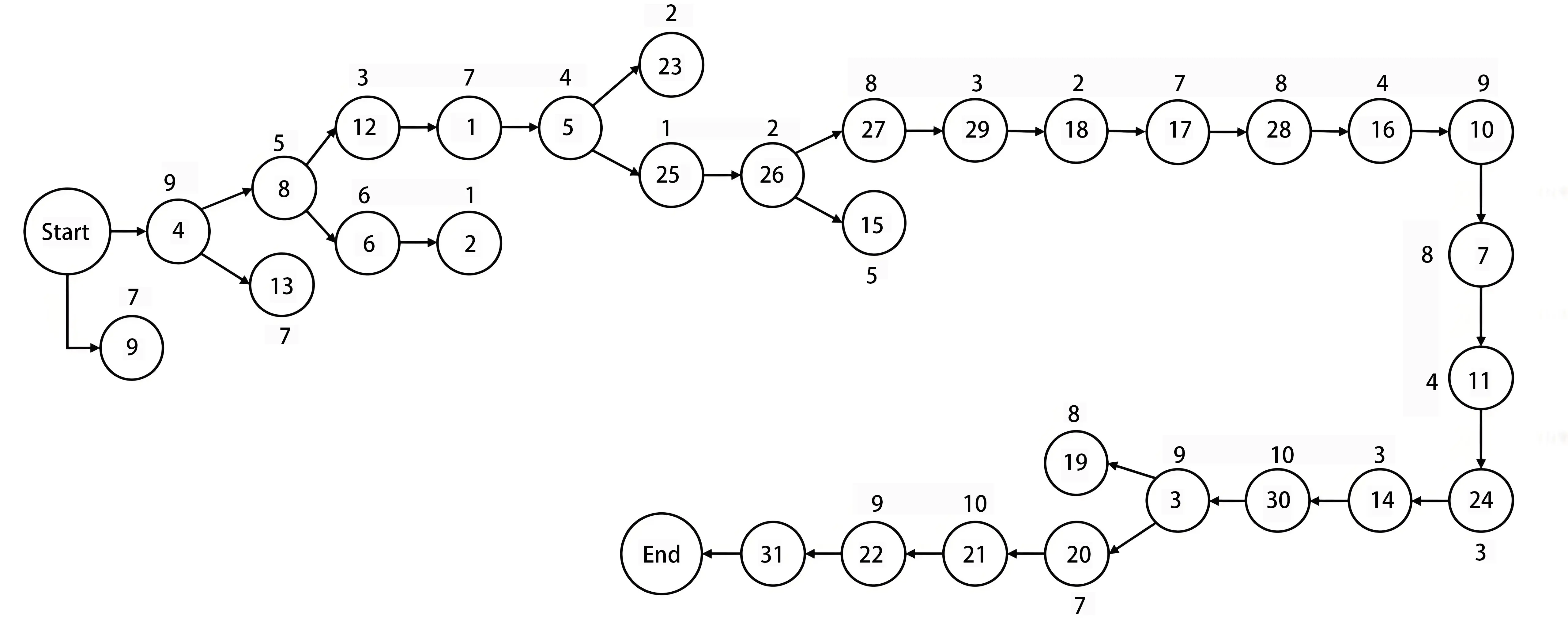
Figure 3. Example of AON diagram for PPO-based solution. AON: arrow on node; PPO: proximal policy optimisation.
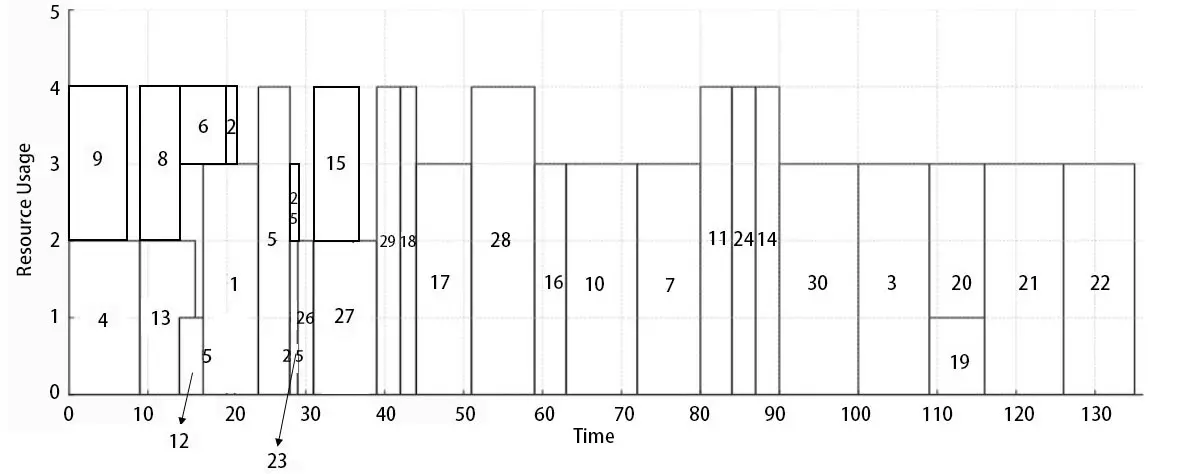
Figure 4. Example of PPO-based schedule optimisation visualisation. PPO: proximal policy optimisation.
The visualisations provide managerial insights beyond computational optimisation. Specifically, the PPO-based schedules demonstrate a more balanced distribution of skilled resources, leading to visibly reduced idle times and smoother task transitions across activities. The denser, continuous allocation patterns in the resource charts indicate enhanced labour utilisation and minimised downtime between dependent tasks. From a managerial standpoint, such improvements imply more efficient workforce coordination, better alignment of multi-skilled teams, and potentially reduced project delays. These findings illustrate how the proposed optimisation framework not only shortens the makespan computationally but also supports practical decision-making for resource planning and on-site scheduling.
The comparison results underscore the strength of policy-gradient RL in this domain. Prior work has similarly observed that DRL methods often outperform traditional heuristics and search algorithms in complex scheduling tasks[65]. In a recent study, Zhao et al.[54] proposed an end-to-end DRL method to train high-quality priority rules and solve RCPSP. The study reported that the utilised PPO-based approach outperforms manually-designed priority rules and is competitive with the state-of-the-art genetic programming-based hyper-heuristics. Cai et al.[17] also suggested that PPO is competitive with and outperforms some existing approaches, such as Latest finishing time, Latest starting time, etc. The findings of our study echo with the previous studies. By learning a dynamic assignment policy, the PPO approach more flexibly adapts to the MSRCPSP structure than fixed-rule or population-based methods, yielding faster convergence and better solutions.
A key advantage of the PPO approach is its ability to explicitly model the project’s skill constraints and dynamic decision process. In our experiment, the state representation of the agent includes resource skill profiles and the current partial schedule, and the reward is shaped to minimise the makespan. This enables PPO to reason directly in the combinatorial space of skill allocation and sequence decisions, rather than relying on manually designed heuristic algorithms. The policy network learns how different skill combinations affect project duration, enabling it to choose resource allocations that satisfy skill requirements while minimising idle time. In contrast, classical metaheuristics must explore many candidate schedules without embedded domain knowledge, which often leads to slower convergence. According to the performance comparison, while both DQN and PPO are DRL-based agents, PPO slightly outperforms DQN in solving MSRCPSP. The PPO agent learns to navigate the joint space of skill assignments and task orderings in a data-driven way, capturing interactions between skills and activity timing that are hard to encode in traditional algorithms. This flexibility of a learned policy is difficult to achieve with value-based methods like DQN in large action spaces. This is also supported by Herrmann and Schaub[66], who compared multiple RL algorithms on a satellite scheduling problem and found that PPO achieves fast, stable convergence to high-performing policies, while DQN can reach good solutions but with much higher variance across different runs and parameter settings.
Regarding the benchmark solutions provided in the MSLIB dataset[64], the developers claimed that any generated schedule within 1 to 1.2 times the given solution can be considered satisfactory. Yet, the heuristic and RL-based algorithms we utilised in this study provide more optimal makespans for some instances, which are shorter than the given deadline. While Anand et al.[67] claimed that CPLEX is one of the most advanced and accepted optimisation solvers, and can provide competitive results on real-life problems, the phenomenon could be possible due to several potential reasons. Firstly, generating exact solutions within a limited time is only possible for small instances, and exact solvers may struggle with larger instances[68,69]. The branch‑and‑cut search of CPLEX must explore a huge solution space, which often enumerates many node relaxations and can be time-consuming. In addition, since the PPO agent is pre-trained, solving new instances is just inference through a neural network. This inference is considered computationally cheaper and faster, whereas CPLEX must solve a full mixed-integer linear programming model from scratch every time. Thus, CPLEX may only find a suboptimal schedule within a time limit of 60 seconds. In contrast, the PPO agent is an approximate, data-driven heuristic. It does not attempt to prove optimality but instead focuses on finding good schedules efficiently. Moreover, as mentioned in the instruction document[64], if CPLEX cannot find a solution within 60 seconds, a naive method shall be used for finding solutions, which may result in generating less considerate and suboptimal solutions. Therefore, possibilities exist for generating more optimal schedules using RL and DRL-based approaches.
While our study demonstrates the feasibility of utilising DRL for MSRCPSP, several important limitations should be acknowledged that may guide future research. Firstly, the training and testing datasets were limited to instances requiring only one skill per activity. In real construction projects, many tasks demand multiple concurrent skills. Extending our RL framework to handle more complex multi-skill requirements will bring our approach closer to solving problems in real-life scenarios. Secondly, this study assumes fixed, known task durations. However, in practice, durations are subject to uncertainty due to weather, supply delays, or unanticipated site conditions. Incorporating stochastic task times, for instance, via a Partially Observable Markov Decision Process, could improve the robustness of learned scheduling policies under real-world variability. In addition, this work restricts precedence relations to simple finish-to-start links. Modern projects often feature more complex dependencies, such as start-to-start, finish-to-finish, resource calendars, and dynamic availability windows. Moreover, this study focused on minimising makespan while considering the skill level requirements of activities. However, construction managers balance multiple objectives in practical projects, such as labour cost, equipment utilisation, contractor preferences, and risk exposure. This is also considered as a limitation by Zarei et al.[70]. Future research can extend the reward function to a multi-objective setting, exploring scalarisation techniques to develop trade-off schemes based on activity priorities.
5. Conclusion
Classified as NP-hard, the MSRCPSP jointly determines activity schedules and allocations of multi-skilled resources. Unlike RCPSP, each activity in the MSRCPSP specifies the skills it requires, rather than anonymous resource units. This study addresses MSRCPSP by formulating activity scheduling as a Markov Decision Process and comparing the scheduling performances of five optimisation agents, including GA, PSO, BKA, DQN, and PPO, on benchmark instances from the MSLIB library. Visual analyses revealed that PPO and DQN solutions clustered closer to the near-optimal baselines, where PPO provided the highest number of optimal or near-optimal solutions and the shortest schedules. Notably, the DRL-based agents also provide more optimal schedules than the benchmark solutions in some instances, potentially due to the restricted performance of the CPLEX optimiser caused by time limitations. Technically, the comparative experiments in this study offer a practical benchmark of widely used heuristics and metaheuristics against DRL baselines, informing future algorithm selection and hybridisation strategies for solving the MSRCPSP. Practically, the application of DRL techniques enables faster schedule planning and better resource utilisation when solving the MSRCPSP, which can reduce any delay caused by unexpected interruptions in practical construction projects. Future studies may extend the RL-based framework to activities requiring multiple concurrent skills, moving beyond the single-skill-per-activity assumption to better reflect real projects. Besides, researchers could also consider incorporating stochastic task durations to improve the robustness of learned policies under weather, supply, and site variability.
Authors contribution
Zhang Y: Conceptualization, methodology, data curation, writing-original draft, formal analysis, writing-review & editing.
Chang R: Conceptualization, methodology, supervision, writing-review & editing, project administration.
Omrany H, Zuo J: Methodology, supervision, writing-review & editing.
Gu N, Burry J: Supervision, writing-review & editing.
Conflicts of interest
Ruidong Chang is an Editorial Board Member of the Journal of Building Design and Environment. The other authors declare no conflicts of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Availability of data and materials
Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request.
Funding
None.
Copyright
© The Author(s) 2025.
References
-
1. Peng JL, Liu X, Peng C, Shao Y. Multi-skill resource-constrained multi-modal project scheduling problem based on hybrid quantum algorithm. Sci Rep. 2023;13(1):18502.[DOI]
-
2. Ahmed R, Hussain A, Philbin SP. Moderating effect of senior management support on the relationship between schedule delay factors and project performance. Eng Manag J. 2021;34(3):374-393.[DOI]
-
3. Park JE. Schedule delays of major projects: What should we do about it? Transp Rev. 2021;41(6):814-832.[DOI]
-
4. Ghai S, Lakhanpal S, Ramola B, Al-Taee M, Alazzam MB. Natural language processing in solving resource constrained project scheduling problems. In: Proceedings of the 2023 3rd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE); 2023 May 12-13; Greater Noida, India. Piscataway: Institute of Electrical and Electronics Engineers; 2023. p. 256-260.[DOI]
-
5. Manousakis K, Savva G, Papadouri N, Mavrovouniotis M, Christofides A, Kolokotroni N, et al. A practical approach for resource-constrained project scheduling. IEEE Access. 2024;12:12976-12991.[DOI]
-
6. Herrmann JP, Mordaschew V, Tackenberg S. A multi-skill RCPSP variant for persons with disabilities in sheltered workshops. Procedia Comput Sci. 2024;232:1329-1338.[DOI]
-
7. Pritsker AAB, Waiters LJ, Wolfe PM. Multiproject scheduling with limited resources: A zero-one programming approach. Manag Sci. 1969;16(1):93-108.[DOI]
-
8. Đumić M, Šišejković D, Čorić R, Jakobović D. Evolving priority rules for resource constrained project scheduling problem with genetic programming. Future Gener Comput Syst. 2018;86(3):211-221.[DOI]
-
9. Snauwaert J, Vanhoucke M. A classification and new benchmark instances for the multi-skilled resource-constrained project scheduling problem. Eur J Oper Res. 2023;307(1):1-19.[DOI]
-
10. Snauwaert J, Vanhoucke M. A solution framework for multi-skilled project scheduling problems with hierarchical skills. J Sched. 2025;28(3):289-310.[DOI]
-
11. Bahroun Z, As’ad R, Tanash M, Athamneh R. The multi-skilled resource-constrained project scheduling problem: A systematic review and an exploration of future landscapes. Manag Syst Prod Eng. 2024;32(1):108-132.[DOI]
-
12. Hosseinian AH, Baradaran V. A two-phase approach for solving the multi-skill resource-constrained multi-project scheduling problem: A case study in construction industry. Eng Constr Archit Manag. 2021;30(1):321-363.[DOI]
-
13. Hegazy T, Shabeeb AK, Elbeltagi E, Cheema T. Algorithm for scheduling with multiskilled constrained resources. J Constr Eng Manag. 2000;126(6):414-421.[DOI]
-
14. Bellenguez-Morineau O, Néron E. A Branch-and-Bound method for solving multi-skill project scheduling problem. RAIRO Oper Res. 2007;41(2):155-170.[DOI]
-
15. Bellenguez-Morineau O, Néron E. Multi-mode and multi-skill project scheduling problem. In: Artigues E, Demassey S, Néron E, editors. Resource-Constrained Project Scheduling: Models, Algorithms, Extensions and Applications. Hoboken: Wiley; 2008. p. 149-160.[DOI]
-
16. Li YY, Lin J, Wang ZJ. Multi-skill resource constrained project scheduling using a multi-objective discrete Jaya algorithm. Appl Intell. 2021;52(5):5718-5738.[DOI]
-
17. Cai H, Bian Y, Liu L. Deep reinforcement learning for solving resource constrained project scheduling problems with resource disruptions. Robot Comput-Integr Manuf. 2024;85:102628.[DOI]
-
18. Goldberg DE, Holland JH. Genetic algorithms and machine learning. Mach Learn. 1988;3(2):95-99.[DOI]
-
19. Holland JH. Genetic algorithms. Sci Am. 1992;267(1):66-73.[DOI]
-
20. Alhijawi B, Awajan A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol Intell. 2023;17(3):1245-1256.[DOI]
-
21. Kennedy J, Eberhart R. Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks; 1995 Nov 27-Dec 01; Perth, Australia. p. 1942-1948.[DOI]
-
22. Jain M, Saihjpal V, Singh N, Singh SB. An overview of variants and advancements of PSO algorithm. Appl Sci. 2022;12(17):8392.[DOI]
-
23. Wang J, Wang W, Hu X, Qiu L, Zang H. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif Intell Rev. 2024;57(4):98.[DOI]
-
24. Du C, Zhang J, Fang J. An innovative complex-valued encoding black-winged kite algorithm for global optimization. Sci Rep. 2025;15(1):932.[DOI]
-
25. Zhang Z, Wang X, Yue Y. Heuristic optimization algorithm of black-winged kite fused with osprey and its engineering application. Biomimetics. 2024;9(10):595.[DOI]
-
26. Mnih V, Kavukcuoglu K, Silver D, Rusu AA, Veness J, Bellemare MG, et al. Human-level control through deep reinforcement learning. Nature. 2015;518(7540):529-533.[DOI]
-
27. Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O. Proximal policy optimization algorithms. arXiv:1707.06347 [Preprint]. 2017.[DOI]
-
28. Luo PC, Xiong HQ, Zhang BW, Peng JY, Xiong ZF. Multi-resource constrained dynamic workshop scheduling based on proximal policy optimisation. Int J Prod Res. 2021;60(19):5937-5955.[DOI]
-
29. Corecco S, Adorni G, Gambardella LM. Proximal policy optimization-based reinforcement learning and hybrid approaches to explore the cross array task optimal solution. Mach Learn Knowl Extr. 2023;5(4):1660-1679.[DOI]
-
30. Correia I, Lourenço LL, Saldanha-da-Gama F. Project scheduling with flexible resources: Formulation and inequalities. OR Spectr. 2010;34(3):635-663.[DOI]
-
31. Montoya C, Bellenguez-Morineau O, Pinson E, Rivreau D. Branch-and-price approach for the multi-skill project scheduling problem. Optim Lett. 2013;8(5):1721-1734.[DOI]
-
32. Damay J, Quilliot A, Sanlaville E. Linear programming based algorithms for preemptive and non-preemptive RCPSP. Eur J Oper Res. 2007;182(3):1012-1022.[DOI]
-
33. Bettemir ÖH, Sonmez R. Hybrid genetic algorithm with simulated annealing for resource-constrained project scheduling. J Manag Eng. 2015;31(5):04014082.[DOI]
-
34. Liu J, Liu Y, Shi Y, Li J. Solving resource-constrained project scheduling problem via genetic algorithm. J Comput Civ Eng. 2020;34(2):04019055.[DOI]
-
35. Zhou H, Li Y, Xu H, Su Y, Chen L. A self-organizing fuzzy neural network modeling approach using an adaptive quantum particle swarm optimization. Appl Intell. 2022;53(11):13569-13592.[DOI]
-
36. Myszkowski PB, Skowroński ME, Podlodowski Ł. Novel heuristic solutions for multi-skill resource-constrained project scheduling problem. In: Proceedings of the 2013 Federated Conference on Computer Science and Information Systems; 2013 Sep 8-11; Krakow, Poland. Piscataway: IEEE; 2013. p. 159-166. Available from: https://ieeexplore.ieee.org/abstract/document/6643992
-
37. Brooks GH. An algorithm for finding optimal or near optimal solutions to the production scheduling problem. J Indust Eng. 1969;16(1):34-40. Available from: https://www.proquest.com/openview/001fe81b887a5bb430748b9ac0c6e005/1?pq-origsite=gscholar&cbl=18750&diss=y
-
38. Almeida BF, Correia I, Saldanha-da-Gama F. Priority-based heuristics for the multi-skill resource constrained project scheduling problem. Expert Syst Appl. 2016;57:91-103.[DOI]
-
39. Yu Y, Xu Z, Zhao S. A two-stage algorithm based on 12 priority rules for the stochastic distributed resource-constrained multi-project scheduling problem with multi-skilled staff. IEEE Access. 2023;11:29554-29565.[DOI]
-
40. Akbar S, Zubair M, Khan R, Ul Akbar U, Ullah R, Zheng Z. Weighted multi-skill resource constrained project scheduling: A greedy and parallel scheduling approach. IEEE Access. 2024;12:29824-29836.[DOI]
-
41. Campos Ciro G, Dugardin F, Yalaoui F, Kelly R. Open shop scheduling problem with a multi-skills resource constraint: A genetic algorithm and an ant colony optimisation approach. Int J Prod Res. 2015;54(16):4854-4881.[DOI]
-
42. Ali MA, Bhatti AR, Rasool A, Farhan M, Esenogho E. Optimal location and sizing of photovoltaic-based distributed generations to improve the efficiency and symmetry of a distribution network by handling random constraints of particle swarm optimization algorithm. Symmetry. 2023;15(9):1752.[DOI]
-
43. Tang J, Duan H, Lao S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif Intell Rev. 2022;56(5):4295-4327.[DOI]
-
44. Zhang H, Li X, Li H, Huang F. Particle swarm optimization-based schemes for resource-constrained project scheduling. Autom Constr. 2005;14(3):393-404.[DOI]
-
45. Jia Q, Guo Y. Hybridization of ABC and PSO algorithms for improved solutions of RCPSP. J Chin Inst Eng. 2016;39(6):727-734.[DOI]
-
46. Cunha B, Madureira AM, Fonseca B, Coelho D. Deep reinforcement learning as a job shop scheduling solver: A literature review. In: Abraham A, Hanne T, Castillo O, Gandhi N, Rios TN, Hong TP, editors. Hybrid Intelligent Systems. Cham: Springer International Publishing; 2020. p. 350-359.[DOI]
-
47. Park J, Chun J, Kim SH, Kim Y, Park J. Learning to schedule job-shop problems: Representation and policy learning using graph neural network and reinforcement learning. Int J Prod Res. 2021;59(11):3360-3377.[DOI]
-
48. Choi J, Realff MJ, Lee JH. AQ-learning-based method applied to stochastic resource constrained project scheduling with new project arrivals. Int J Robust Nonlinear Control. 2007;17(13):1214-1231.[DOI]
-
49. Jędrzejowicz P, Ratajczak-Ropel E. Reinforcement learning strategies for A-Team solving the resource-constrained project scheduling problem. Neurocomputing. 2014;146:301-307.[DOI]
-
50. Sallam KM, Chakrabortty RK, Ryan MJ. A reinforcement learning based multi-method approach for stochastic resource constrained project scheduling problems. Expert Syst Appl. 2021;169:114479.[DOI]
-
51. Szwarcfiter C, Herer YT, Shtub A. Balancing project schedule, cost, and value under uncertainty: A reinforcement learning approach. Algorithms. 2023;16(8):395.[DOI]
-
52. Zhang Y, Li X, Teng Y, Shen Q, Bai S. A reinforcement learning framework for maximizing the net present value of stochastic multi-work packages project scheduling problem. In: Li D, Zou PXW, Yuan J, Wang Q, Peng Y, editors. Proceedings of the 28th International Symposium on Advancement of Construction Management and Real Estate. 2023 Aug 5-6; Singapore: Springer Nature Singapore; 2024. p. 733-756.[DOI]
-
53. Li Y. Deep reinforcement learning: An overview. arXiv:1701.07274 [Preprint]. 2017. Available from: https://doi.org/10.48550/arXiv.1701.07274
-
54. Zhao X, Song W, Li Q, Shi H, Kang Z, Zhang C. A deep reinforcement learning approach for resource-constrained project scheduling. In: Ishibuchi H, Kwoh CK, Tan AH, Srinivasan D, Miao C, Trivedi A, Crockett K, editors. Proceedings of the 2022 IEEE Symposium Series on Computational Intelligence (SSCI); 2022 Dec 4-7; Singapore, Singapore. Piscataway: Institute of Electrical and Electronics Engineers; 2022. p. 1226-1234.[DOI]
-
55. Liu H, Zhang J, Zhang X, Chen Z. A new resource-constrained project scheduling problem with ladder-type carbon trading prices and its algorithm based on deep reinforcement learning. Expert Syst Appl. 2024;255:124794.[DOI]
-
56. Herroelen W, De Reyck B, Demeulemeester E. Resource-constrained project scheduling: A survey of recent developments. Comput Oper Res. 1998;25(4):279-302.[DOI]
-
57. Ding H, Zhuang C, Liu J. Extensions of the resource-constrained project scheduling problem. Autom Constr. 2023;153:104958.[DOI]
-
58. Deb K, Agrawal RB. Simulated binary crossover for continuous search space. Complex syst. 1995;9(2):115-148.[DOI]
-
59. Li C, Zhang K, Zheng B, Chen Y. Path planning problem solved by an improved black-winged kite optimization algorithm based on multi-strategy fusion. Int J Mach Learn Cybern. 2025;16(10):7859-7895.[DOI]
-
60. Mohapatra S, Kaliyaperumal D, Gharehchopogh FS. A revamped black winged kite algorithm with advanced strategies for engineering optimization. Sci Rep. 2025;15(1):17681.[DOI]
-
61. Hessel M, Modayil J, Van Hasselt H, Schaul T, Ostrovski G, Dabney W, et al. Rainbow: Combining improvements in deep reinforcement learning. In: Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence; 2018 Feb 2-7; New Orleans, USA. Menlo Park: AAAI; 2018.[DOI]
-
62. Schulman J, Moritz P, Levine S, Jordan M, Abbeel P. High-dimensional continuous control using generalized advantage estimation. arXiv:1506.02438 [Preprint]. 2015. Available from: https://doi.org/10.48550/arXiv.1506.02438
-
63. Myszkowski PB, Skowroński ME, Olech ŁP, Oślizło K. Hybrid ant colony optimization in solving multi-skill resource-constrained project scheduling problem. Soft Comput. 2014;19(12):3599-3619.[DOI]
-
64. Snauwaert J, Vanhoucke M. MSRCPSP Data files: The Patterson format, Operations Research & Scheduling Research Group. 2025. Available from: https://www.projectmanagement.ugent.be/research/project_scheduling/MSRCPSP
-
65. Vivekanandan D, Wirth S, Karlbauer P, Klarmann N. A reinforcement learning approach for scheduling problems with improved generalization through order swapping. Mach Learn Knowl Extr. 2023;5(2):418-430.[DOI]
-
66. Herrmann A, Schaub H. A comparative analysis of reinforcement learning algorithms for earth-observing satellite scheduling. Front Space Technol. 2023;4:1263489.[DOI]
-
67. Anand R, Aggarwal D, Kumar V. A comparative analysis of optimization solvers. J Stat Manag Syst. 2017;20(4):623-635.[DOI]
-
68. Karimi-Mamaghan M, Mohammadi M, Meyer P, Karimi-Mamaghan AM, Talbi EG. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: A state-of-the-art. Eur J Oper Res. 2022;296(2):393-422.[DOI]
-
69. Zhang J, Ding G, Zou Y, Qin S, Fu J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J Intell Manuf. 2017;30(4):1809-1830.[DOI]
-
70. Zarei F, Arashpour M, Mirnezami SA, Shahabi-Shahamiri R, Ghasemi M. Multi-skill resource-constrained project scheduling problem considering overlapping: Fuzzy multi-objective programming approach to a case study. Int J Constr Manag. 2023;24(8):820-833.[DOI]
Copyright
© The Author(s) 2025. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Publisher’s Note
Share And Cite




